题目内容
1.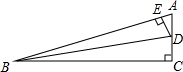 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.(1)求AC,CD的长;
(2)求tan∠DBC的值.
分析 (1)在Rt△ADE中先利用余弦的定义计算出AD=26,再利用勾股定理计算出DE=24,接着根据角平分线的性质得CD=ED=24,则AC=AD+CD=50;
(2)先在Rt△ADE中,计算出tanA=$\frac{24}{10}$=$\frac{12}{5}$,则在Rt△ABC中,利用正切可求出BC=120,然后在Rt△BDC中,根据正切的定义求tan∠DBC.
解答 解:(1)在Rt△ADE中,∵cosA=$\frac{AE}{AD}$=$\frac{5}{13}$,
∴AD=$\frac{13}{5}$AE=26,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{2{6}^{2}-1{0}^{2}}$=24,
∵BD是∠ABC的平分线,DE⊥AB,DC⊥BC,
∴CD=ED=24,
∴AC=AD+CD=26+24=50;
(2)在Rt△ADE中,tanA=$\frac{DE}{AE}$=$\frac{24}{10}$=$\frac{12}{5}$,
在Rt△ABC中,∵tanA=$\frac{BC}{AC}$=$\frac{12}{5}$,
∴BC=120,
在Rt△BDC中,tan∠DBC=$\frac{DC}{BC}$=$\frac{24}{120}$=$\frac{1}{5}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了角平分线的性质和勾股定理.

练习册系列答案
相关题目
6.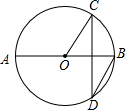 如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
 如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
13.不等式x+1>3的解集是( )
| A. | x>1 | B. | x>-2 | C. | x>2 | D. | x<2 |

 ,
, ,则
,则 的值是_________.
的值是_________. 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD.
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )