题目内容
6.已知:△ACB为等腰直角三角形,点P在AC上,连BP,过B点作BE⊥BP,BE=PB,连AE交BC于F.(1)如图1,问PA与CF有何数量关系,并证明;
(2)如图2,若点P在CA的延长线上,问上结论是否仍成立,画图证明.

分析 (1)如图1作EM⊥BC,先证明CM=AP,再证明CM=2CF即可.
(2)和(1)类似.
解答 解:(1)结论:PA=2CF,理由如下: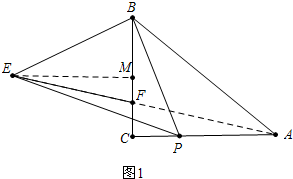 作EM⊥BC垂足为M,
作EM⊥BC垂足为M,
∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
$\left\{\begin{array}{l}{∠EBM=∠CPB}\\{∠EMB=∠BCP}\\{EB=BP}\end{array}\right.$,
∴△EBM≌△BPC,
∴BM=CP,EM=BC,
∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴$\frac{EM}{AC}=\frac{MF}{CF}$,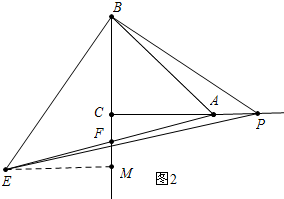
∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
(2)结论不变,如图2,
证明:作EM⊥BC垂足为M,
∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
$\left\{\begin{array}{l}{∠EBM=∠CPB}\\{∠EMB=∠BCP}\\{EB=BP}\end{array}\right.$,
∴△EBM≌△BPC,
∴BM=CP,EM=BC,∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴$\frac{EM}{AC}=\frac{MF}{CF}$,
∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
点评 本题考查全等三角形的判定和性质、平行线分线段成比例定理,添加辅助线构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
13.不等式x+1>3的解集是( )
| A. | x>1 | B. | x>-2 | C. | x>2 | D. | x<2 |
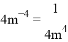 ;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( )
;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( )
 如图,已知DE⊥AB于E,∠D=∠B,EA=EF,求证:
如图,已知DE⊥AB于E,∠D=∠B,EA=EF,求证: 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2). 如图所示.
如图所示. ,
, ,则
,则 的值是_________.
的值是_________.