题目内容
2. 如图,AB是⊙O的直径,C是⊙O上一点,且BC=3,AC=5,CP平分∠ACB交⊙O于点P,交直径AB于点D,则线段CP的长为4$\sqrt{2}$.
如图,AB是⊙O的直径,C是⊙O上一点,且BC=3,AC=5,CP平分∠ACB交⊙O于点P,交直径AB于点D,则线段CP的长为4$\sqrt{2}$.
分析 根据圆周角定理及勾股定理可得AP的长,过D作DF⊥AC于F,DG⊥BC于G,F,G是垂足,则四边形CFDG是正方形,设DF=DG=x,由三角形面积公式可求出x的值,及CD的值,根据△APD∽△CBD,根据相似比可求出PD的长,进而求出CP的长.
解答 解:连接AP,BP,∵AB是直径,
∴∠ACB=90°,
∵BC=3,AC=5,
∴AB=$\sqrt{34}$,
∵CD平分∠ACB,
∴$\widehat{AP}=\widehat{BP}$,
∴AP=BP=$\sqrt{17}$,
过D作DF⊥AC于F,DG⊥BC于G,F,G是垂足,则四边形CFDG是正方形,
设DF=DG=x,
∴$\frac{1}{2}$AC•x+$\frac{1}{2}$BC•x=$\frac{1}{2}$AC•BC,
∴$\frac{1}{2}$×5•x+$\frac{1}{2}$×3x=$\frac{1}{2}$×5×3,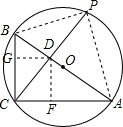
∴x=$\frac{15}{8}$,
∴CD=$\frac{15\sqrt{2}}{8}$,AD=$\sqrt{(\frac{15}{8})^{2}+(5-\frac{15}{8})^{2}}$=$\frac{5\sqrt{34}}{8}$,
∴BD=AB-AD=$\frac{3\sqrt{34}}{8}$,
∵∠PAB=∠PCB,
∵△APD∽△CBD,
∴PD:BD=AP:BC,
∴PD:$\frac{3\sqrt{34}}{8}$=$\sqrt{17}$:3,
∴PD=$\frac{17\sqrt{2}}{8}$,
∴PC=CD+PD=$\frac{15\sqrt{2}}{8}$+$\frac{17\sqrt{2}}{8}$=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题综合考查了圆周角定理,垂径定理,角平分线的性质,及相似三角形的性质.解答此题的关键是作出辅助线,构造正方形.

 字词句段篇系列答案
字词句段篇系列答案| A. | (1,-3) | B. | (2,-2) | C. | (3,-3) | D. | (2,-4) |

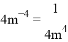 ;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( )
;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( ) 如图,在四边形ABCD中,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
如图,在四边形ABCD中,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2). 如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD.
如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端A重合,测得BC=9.2m,CA=0.8m,求树的高度BD.