题目内容
18.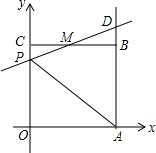 如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.(1)求点D的坐标(用含m的代数式表示);
(2)当AP=AD时,求m的值;
(3)当PD=PA时,求m的值.
分析 (1)首先证明△PCM≌△DBM,即可得到PC=BD,结合正方形的性质以及点P的坐标特点进而求出点D的坐标;
(2)若AP=AD,先根据勾股定理求出AP的长,进而列出m的一元一次方程求出m的值;
(3)过P作PE⊥AB于点E,根据PD=PA可得到AE=DE,结合AE=OP列出m的方程,求出m的值.
解答 解:(1)∵M是BC的中点,
∴CM=BM,
在△PCM和△DBM中,
$\left\{\begin{array}{l}{∠PCM=∠DBM}\\{CM=BM}\\{∠CMP=∠BMD}\end{array}\right.$,
∴△PCM≌△DBM,
∴PC=BD,
∵点P(0,m),
∴PC=BD=2-m,
∴AD=4-m,
∴点D坐标为(2,4-m);
(2)若AP=AD,
则OA2+OP2=AP2=AD2,
即4+m2=(4-m)2, 解得m=$\frac{3}{2}$;
解得m=$\frac{3}{2}$;
(3)若PD=PA,过P作PE⊥AB于点E,如图,
则AE=ED=$\frac{1}{2}$AD=$\frac{1}{2}$(4-m),
又知OP=AE,
即m=$\frac{1}{2}$(4-m),
解得m=$\frac{4}{3}$.
点评 本题主要考查了四边形的知识,此题涉及到全等三角形的判断与性质、点的坐标、勾股定理以及正方形的性质等知识,解答本题的关键是熟练掌握勾股定理求边长等知识,此题难度不大.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9.如图,数轴上有一个质点从原点出发,沿数轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动,质点落在表示数3的点上(允许重复过此点),则质点的不同运动方案共有( )

| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
6.若抛物线y=(a-1)x2-2x+3与x轴有交点,则整数a的最大值是( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
13.关于x的二次方程ax2+bx-c=0的两个根是x1=m,x2=n,那么二次函数y=-ax2-bx+c与x轴的两个交点的坐标是( )
| A. | (m,0)(n,0) | B. | (m,0)(-n,0) | C. | (-m,0)(n,0) | D. | (-m,0)(-n,0) |