题目内容
13.关于x的二次方程ax2+bx-c=0的两个根是x1=m,x2=n,那么二次函数y=-ax2-bx+c与x轴的两个交点的坐标是( )| A. | (m,0)(n,0) | B. | (m,0)(-n,0) | C. | (-m,0)(n,0) | D. | (-m,0)(-n,0) |
分析 令y=0得:-ax2-bx+c=0,整理得:ax2+bx-c=0,由已知条件可得到二次函数y=-ax2-bx+c与x轴的两个交点的坐标.
解答 解:令y=0得:-ax2-bx+c=0,
整理得:ax2+bx-c=0,
∵方程ax2+bx-c=0的两个根是x1=m,x2=n,
∴二次函数y=-ax2-bx+c与x轴的两个交点的坐标(m,0)(n,0).
故选:A.
点评 本题主要考查的是抛物线与x轴的交点,将函数问题转化为方程问题是解题的关键.

练习册系列答案
相关题目
5. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )| A. | 4cm2 | B. | 3cm2 | C. | 2cm2 | D. | 1cm2 |
 作图题:已知:直线a和直线外一点A,过A点作直线a的平行线.
作图题:已知:直线a和直线外一点A,过A点作直线a的平行线. 已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,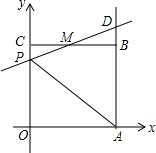 如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.