题目内容
6.若抛物线y=(a-1)x2-2x+3与x轴有交点,则整数a的最大值是( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
分析 令y=0得(a-1)x2-2x+3=0,然后由△≥0求得a的取值范围,然后可确定出a的值.
解答 解:令y=0得:(a-1)x2-2x+3=0,
∵抛物线y=(a-1)x2-2x+3与x轴有交点,
∴方程(a-1)x2-2x+3=0有实数根.
∴△≥0,即4-12(a-1)≥0.
解得:a≤$\frac{4}{3}$.
∴a的最大整数值为1.
故选:B.
点评 本题主要考查的是抛物线与x轴的交点,将函数问题转化为方程问题是解题的关键.

练习册系列答案
相关题目
14.在△ABC中,∠B=45°,∠C=60°,BC边上的高AD=3,则BC的长为( )
| A. | 3+3$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$+$\sqrt{6}$ |
11.下列关系式中,属于二次函数的是(x是自变量)( )
| A. | y=$\frac{1}{3}{x}^{2}$ | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=ax2+bx+c |
16.下列一元二次方程中适合用因式分解法解的是( )
| A. | x2+x+1=0 | B. | 2x2-3x+5=0 | C. | x2-7x=8 | D. | x2+6x+7=0 |
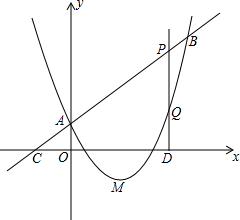 已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合).
已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合). 作图题:已知:直线a和直线外一点A,过A点作直线a的平行线.
作图题:已知:直线a和直线外一点A,过A点作直线a的平行线.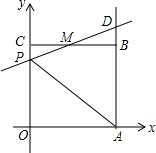 如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.