题目内容
3．现有一个多边形，其内角和为1620°，则该多边形有11个内角．分析 设该多边形的边数为n，则根据多边形内角和定理得到（n-2）×180°=1620°，然后解方程即可．
解答 解：设该多边形的边数为n，
根据题意得（n-2）×180°=1620°，
解得n=11．
即该多边形的边数为11，多边形有11个内角．
故答案为11．
点评 本题考查了多边形内角与外角：内角和定理：（n-2）．•80 （n≥3）且n为整数）；多边形的外角和等于360度．
练习册系列答案
相关题目
14．在△ABC中，∠B=45°，∠C=60°，BC边上的高AD=3，则BC的长为（ ）
| A． | 3+3$\sqrt{3}$ | B． | 3+$\sqrt{3}$ | C． | 2+$\sqrt{3}$ | D． | $\sqrt{3}$+$\sqrt{6}$ |
11．下列关系式中，属于二次函数的是（x是自变量）（ ）
| A． | y=$\frac{1}{3}{x}^{2}$ | B． | y=$\sqrt{{x}^{2}-1}$ | C． | y=$\frac{1}{{x}^{2}}$ | D． | y=ax2+bx+c |
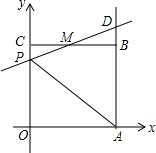如图，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点．P（0，m）是线段OC上以一动点（C点除外）．直线PM交AB的延长线于点D．
8．
图中几何体的截面的形状图是（ ）
图中几何体的截面的形状图是（ ）| A． |  | B． |  | C． |  | D． |  |