题目内容
9.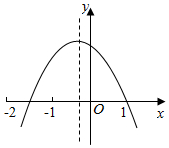 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )①c>0;②a<b<0;③2b+c>0;④当x>-$\frac{1}{2}$时,y随x的增大而减小.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 设y=ax2+bx+c与x轴的交点为A,B,左边为A,右边为B,A(x1,0),B(x2,0),那么抛物线方程可写为y=a(x-x1)(x-x2),那么b=-a(x1+x2),从图中可知,因为x1+x2>-1,因此b=-a(x1+x2)>(-a)×(-1)=a,所以a<b<0,故②正确,其余不难判断.
解答 解:由图象可知,a<0,c>0,a+b+c=0,a-b+c>0,故①正确,
设y=ax2+bx+c与x轴的交点为A,B,左边为A,右边为B,A(x1,0),B(x2,0),那么抛物线方程可写为y=a(x-x1)(x-x2),那么b=-a(x1+x2),从图中可知,因为x1+x2>-1,因此b=-a(x1+x2)>(-a)×(-1)=a,
所以a<b<0,故②正确,
∵a+b+c=0,a<b<0,
∴2b+c>0,故③正确,
由图象可知,抛物线与x轴的两个交点,一个是1,一个在-2与-1之间,因此,对称轴必在-1/2与0之间,x>-$\frac{1}{2}$这一范围内必存在着-1/2<x<-b/2a,在此区间y随x的增大而增大故④错误.
故选C.
点评 本题考查二次函数的图象与系数的关系,灵活运用二次函数的性质是解题的关键,属于中考常考题型.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
20. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{2}$ |
 如图,已知点A、B是数轴上的两点,O为原点,点B对应的数为3,AB=10.
如图,已知点A、B是数轴上的两点,O为原点,点B对应的数为3,AB=10.