题目内容
20. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{2}$ |
分析 根据直角三角形的性质求出AB、BC的长,根据旋转的性质、等边三角形的性质、勾股定理计算即可.
解答 解:∵∠C=90°,∠ABC=30°,AC=2,
∴AB=4,∠A=60°,
由勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
由旋转的性质可知,CA=CA′,由∠A=60°,
∴△ACA′是等边三角形,
∴AA′=2,
∴A′B=2,
由旋转的性质可知,△B1BC是等边三角形,
∴BB1=2$\sqrt{3}$,
∴BD=$\sqrt{3}$,
由勾股定理得,A1D=$\sqrt{7}$
故选:A.
点评 本题考查的是旋转的性质,等边三角形的性质以及勾股定理的应用,掌握旋转前、后的图形全等是解题的关键.

练习册系列答案
相关题目




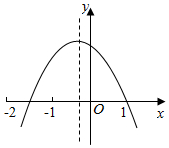 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )