题目内容
14. 如图,已知点A、B是数轴上的两点,O为原点,点B对应的数为3,AB=10.
如图,已知点A、B是数轴上的两点,O为原点,点B对应的数为3,AB=10.(1)填空:数轴上点A表示的数是-7;
(2)动点P从O出发以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)
①当动点P在线段AB上时,则AP=7-3t(用含t的代数式表示);
②是否存在t值,使得BP=5AP成立?若存在,求出t的值;若不存在,说明理由.
分析 (1)根据图形可知:A在B的左边,由AB的长可以得出OA的长,从而得出数轴上点A表示的数;
(2)①速度为3,时间为t,则路程OP=3t,所以AP=AO-OP,代入可得结果;
②分两种情况:根据等量关系式BP=5AP分别列方程可得结论.
解答 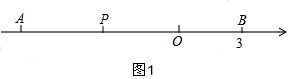 解:(1)∵点B对应的数为3,
解:(1)∵点B对应的数为3,
∴OB=3,
∵AB=10,
∴OA=7,
∵点A在原点的左边,
∴数轴上点A表示的数是-7;
故答案为:-7;
(2)①如图1,由题意得:OP=3t,则AP=OA-OP=7-3t=7-3t,
故答案为:7-3t;
②存在,分两种情况:
i)当P在线段AB上时,如图1,
若BP=5AP成立,则3t+3=5(7-3t),
t=$\frac{16}{9}$;
ii)当P在线段AB外时,如图2,
若BP=5AP成立,则3+3t=5(3t-7),
t=$\frac{19}{6}$;
∴存在这样的t值,t的值是$\frac{16}{9}$或$\frac{19}{6}$.
点评 本题考查了一元一次方程的应用、数轴上两点的距离及数轴,根据已知得出的各线段的长列等量关系式是要本题的关键.

练习册系列答案
相关题目
9.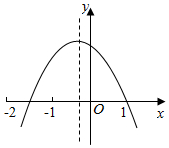 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
①c>0;②a<b<0;③2b+c>0;④当x>-$\frac{1}{2}$时,y随x的增大而减小.
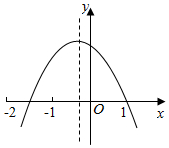 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )①c>0;②a<b<0;③2b+c>0;④当x>-$\frac{1}{2}$时,y随x的增大而减小.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.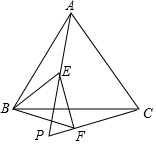 已知边长为4的等边△ABC,E,F分别是AB、BC的中点,将△BEF绕点B顺时针旋转α°,AE与CF交于P.当α=60°时,点P运动的路径长是( )
已知边长为4的等边△ABC,E,F分别是AB、BC的中点,将△BEF绕点B顺时针旋转α°,AE与CF交于P.当α=60°时,点P运动的路径长是( )
 已知边长为4的等边△ABC,E,F分别是AB、BC的中点,将△BEF绕点B顺时针旋转α°,AE与CF交于P.当α=60°时,点P运动的路径长是( )
已知边长为4的等边△ABC,E,F分别是AB、BC的中点,将△BEF绕点B顺时针旋转α°,AE与CF交于P.当α=60°时,点P运动的路径长是( )| A. | $\frac{1}{6}$π | B. | $\frac{4}{3}$π | C. | $\frac{2\sqrt{3}}{9}$π | D. | $\frac{4\sqrt{3}}{9}$π |
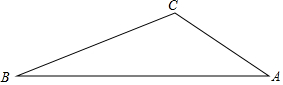 如图,在△ABC中,∠B=30°,AC=2$\sqrt{3}$,BC=6,求sinA的值.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{3}$,BC=6,求sinA的值.