��Ŀ����
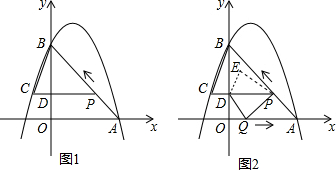
16����ͼ1�����κ���y=-x2+bx+c��ͼ�����A��3��0����B��0��4�����㣬����P��A���������߶�AB����A��B�ķ�����ÿ��2����λ���ȵ��ٶ��˶�������P��PD��y�ڵ�D�����������ڵ�C�����˶�ʱ��Ϊt���룩����1������κ���y=-x2+bx+c�ı���ʽ��
��2������BC����t=$\frac{5}{6}$ʱ�����BCP�������
��3����ͼ2������P��A����ʱ������Qͬʱ��O���������߶�OA����O��A�ķ�����1����λ���ȵ��ٶ��˶�������P��B�غ�ʱ��P��Q����ͬʱֹͣ�˶�������DQ��PQ������DPQ��ֱ��PC�۵��õ���DPE�����˶������У����DPE�͡�OAB�غϲ��ֵ����ΪS��ֱ��д��S��t�ĺ�����ϵ��t��ȡֵ��Χ��
���� ��1��ֱ�ӽ�A��B�������������з����������ɣ�
��2����ͼ1��Ҫ�����BCP��������������Ӧ�ĵߣ���PC��BD������OD������BD��PC�����õ�P�͵�C�ĺ����������Ҫע����ţ�
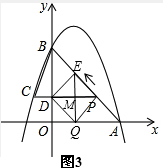
��3��������������ۣ��١�DPE��ȫ�ڡ�OAB��ʱ������0��t��$\frac{15}{17}$ʱ����ͼ2��ʾ���غϲ��ֵ����ΪS���ǡ�DPE��������ڡ�DPE��һ�����ڡ�OAB��ʱ����$\frac{15}{17}$��t��2.5ʱ����ͼ4��ʾ����PDN�����غϲ��ֵ����S��
���  �⣺��1����A��3��0����B��0��4������y=-x2+bx+c�еã�
�⣺��1����A��3��0����B��0��4������y=-x2+bx+c�еã�
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=4}\end{array}\right.$ ���$\left\{\begin{array}{l}{b=\frac{5}{3}}\\{c=4}\end{array}\right.$��
����κ���y=-x2+bx+c�ı���ʽΪ��y=-x2+$\frac{5}{3}$x+4��
��2����ͼ1����t=$\frac{5}{6}$ʱ��AP=2t��
��PC��x�ᣬ
��$\frac{OB}{OD}=\frac{AB}{AP}$��
��$\frac{4}{OD}=\frac{5}{2t}$��
��OD=$\frac{8t}{5}$=$\frac{8}{5}$��$\frac{5}{6}$=$\frac{4}{3}$��
��y=$\frac{4}{3}$ʱ��$\frac{4}{3}$=-x2+$\frac{5}{3}$x+4��
3x2-5x-8=0��
x1=-1��x2=$\frac{8}{3}$��
��C��-1��$\frac{4}{3}$����
��$\frac{BD}{OB}=\frac{PD}{OA}$��$\frac{4-\frac{4}{3}}{4}=\frac{PD}{3}$��
��PD=2��
��S��BCP=$\frac{1}{2}$��PC��BD=$\frac{1}{2}$��3��$\frac{8}{3}$=4��
��3����ͼ3��
����E��AB��ʱ��
�ɣ�2����OD=QM=ME=$\frac{8t}{5}$��
��EQ=$\frac{16t}{5}$��
���۵��ã�EQ��PD����EQ��y��
��$\frac{EQ}{OB}=\frac{AQ}{OA}$��
��$\frac{\frac{16t}{5}}{4}=\frac{3-t}{3}$��
��t=$\frac{15}{17}$��
ͬ���ã�PD=3-$\frac{6t}{5}$��
�൱0��t��$\frac{15}{17}$ʱ��S=S��PDQ=$\frac{1}{2}$��PD��MQ=$\frac{1}{2}$����3-$\frac{6t}{5}$����$\frac{8t}{5}$��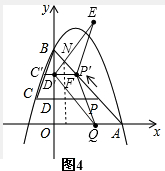
S=-$\frac{24}{25}$t2+$\frac{12}{5}$t��
��$\frac{15}{17}$��t��2.5ʱ��
��ͼ4��P��D��=3-$\frac{6t}{5}$��
��Q���E����ֱ��P��C��Գƣ���Q��t��0����E��t��$\frac{16t}{5}$����
��AB�Ľ���ʽΪ��y=-$\frac{4}{3}$x+4��
D��E�Ľ���ʽΪ��y=$\frac{8}{5}$x+$\frac{8}{5}$t��
��N��$\frac{15-6t}{11}$��$\frac{8t+24}{11}$����
��S=S��P��D��N=$\frac{1}{2}$��P��D���FN=$\frac{1}{2}$����3-$\frac{6t}{5}$����$\frac{8t+24}{11}$-$\frac{8t}{5}$����
��S=$\frac{144}{275}$t2-$\frac{144}{55}$t+$\frac{36}{11}$��
���� �����Ƕ��κ������ۺ��⣬���������ô���ϵ��������κ�����һ�κ����Ľ���ʽ���������÷����������ͼ��Ľ��㣬�ѷ��̺ͺ����л��ؽ����һ��ʹ�����������ͬʱ�����˷������۵�˼�룬��һ˼���ڶ��κ����о������ã�Ҫ�������գ���������ƽ�ϣ��������������ζ�Ӧ�ߵı�����ʾ�߶εij���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | a2-1 | B�� | a2+a | C�� | a2+a-2 | D�� | ��a+2��2-2��a+2��+1 |
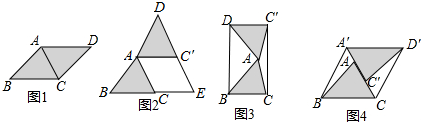
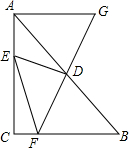 ��ͼ���ڡ�ABC�У�D��AB���е㣬E�DZ�AC��һ���㣬����DE������D��DF��DE����BC�ڵ�F����F���B��C���غϣ����ӳ�FD����G��ʹDG=DF������EF��AG����֪AB=10��BC=6��AC=8��
��ͼ���ڡ�ABC�У�D��AB���е㣬E�DZ�AC��һ���㣬����DE������D��DF��DE����BC�ڵ�F����F���B��C���غϣ����ӳ�FD����G��ʹDG=DF������EF��AG����֪AB=10��BC=6��AC=8��