题目内容
13.己知P是线段AB上一点(与端点A、B不重合),M是线段AP的中点,N是线段BP中点,AB=6厘米,那么MN的长等于( )| A. | 2厘米 | B. | 3厘米 | C. | 4厘米 | D. | 5厘米 |
分析 首先根据中点定义可得到AM=PM=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,再根据图形可得PB=AB-AP,MN=MP+PN,即可得到答案.
解答 解:∵M是AP的中点,
∴AM=PM=$\frac{1}{2}$AP,
∵N是PB的中点,
∴PN=$\frac{1}{2}$PB,
∴MN=MP+PN=$\frac{1}{2}$(AP+PB)=$\frac{1}{2}$AB=3厘米,
故选B.
点评 此题主要考查了求两点间的距离,解题的关键是根据条件理清线段之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.将下列多项式因式分解,结果中不含有因式a+1的是( )
| A. | a2-1 | B. | a2+a | C. | a2+a-2 | D. | (a+2)2-2(a+2)+1 |
5.当a=$\sqrt{2}+1,b=\sqrt{2}$-1时,代数式$\frac{{{a^2}-2ab+{b^2}}}{{{a^2}-{b^2}}}$的值是$\frac{\sqrt{2}}{2}$.
2.在平面直角坐标系中点P(-2,3)和Q(m,n)关于x轴对称,则m的值为( )
| A. | m=-2 | B. | m=2 | C. | m=-3 | D. | m=3 |

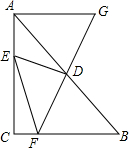 如图,在△ABC中,D是AB的中点,E是边AC上一动点,联结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,联结EF、AG,已知AB=10,BC=6,AC=8.
如图,在△ABC中,D是AB的中点,E是边AC上一动点,联结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,联结EF、AG,已知AB=10,BC=6,AC=8.