题目内容
15.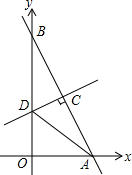 如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.(1)求线段AB的长;
(2)求tan∠DAO的值;
(3)若把△ADC绕点A顺时针旋转α°(0<α<90),点D,C的对应点分别为D1,C1,得到△AD1C1,当AC1∥y轴时,分别求出点C1,点D1的坐标.
分析 (1)先根据方程的解求得线段OA,OB的长,再根据勾股定理求得AB的长;
(2)先根据线段垂直平分线的性质,得到AD=BD,再根据Rt△AOD中的勾股定理,求得OD的长,并计算tan∠DAO的值;
(3)先根据旋转的性质,求得AC1和C1D1的长,再根据OA=4,AC1∥y轴,求得点C1和点D1的坐标.
解答  解:(1)由方程x(x-4)+8(4-x)=0,解得
解:(1)由方程x(x-4)+8(4-x)=0,解得
x1=4,x2=8,
即OA=4,OB=8,
∴由勾股定理可得AB=$4\sqrt{5}$
(2)∵CD为AB的垂直平分线,
∴AD=BD
∵在Rt△AOD中,OD2+OA2=AD2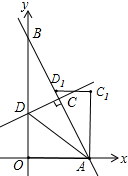
即OD2+42=(8-OD)2,
∴OD=3
∴$tan∠OAD=\frac{3}{4}$
(3)由旋转可得,AC1=AC=2$\sqrt{5}$,C1D1=CD=$\sqrt{{5}^{2}-(2\sqrt{5})^{2}}$=$\sqrt{5}$
又∵OA=4,AC1∥y轴
∴C1(4,$2\sqrt{5}$),D1($4-\sqrt{5}$,$2\sqrt{5}$)
点评 本题主要考查了几何变换中的旋转变换,掌握线段垂直平分线的性质以及利用勾股定理列出方程是解题的关键.在图形旋转时,旋转前、后的图形全等,即对应边相等,对应角也相等.

练习册系列答案
相关题目
4.将下列多项式因式分解,结果中不含有因式a+1的是( )
| A. | a2-1 | B. | a2+a | C. | a2+a-2 | D. | (a+2)2-2(a+2)+1 |
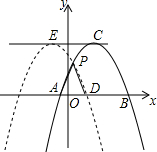 如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
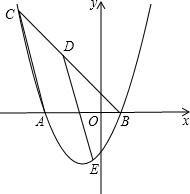 如图,已知抛物线y=$\frac{1}{2}$x2+mx+n与x轴相交于点A、B两点,过点B的直线y=-x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
如图,已知抛物线y=$\frac{1}{2}$x2+mx+n与x轴相交于点A、B两点,过点B的直线y=-x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,