题目内容
17．
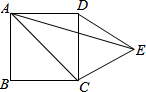如图，在正方形ABCD的外侧，作等边三角形DCE，若∠AED=15°，则∠EAC=（ ）| A． | 15° | B． | 28° | C． | 30° | D． | 45° |
分析 由于四边形ABCD是正方形，△DCE是正三角形，由此可以得到AD=DE，接着利用正方形和正三角形的内角的性质即可求解．
解答 解：∵四边形ABCD是正方形，
∴∠BAD=90°，AB=AD，∠DAC=45°
又∵△DCE是正三角形，
∴DE=AD，∠EDC=60°，
∴△ADE是等腰三角形，∠ADE=90°+60°=150°，
∴∠DAE=∠AED=15°，
∵∠DAC=45°，
∴∠EAC=∠DAC-∠DAE=45°-15°=30
故选C．
点评 此题主要考查了正方形和等边三角形的性质，同时也利用了三角形的内角和，解题首先利用正方形和等边三角形的性质证明等腰三角形，然后利用等腰三角形的性质即可解决问题
练习册系列答案
阅读快车系列答案
相关题目
5．当a=$\sqrt{2}+1，b=\sqrt{2}$-1时，代数式$\frac{{{a^2}-2ab+{b^2}}}{{{a^2}-{b^2}}}$的值是$\frac{\sqrt{2}}{2}$．
2．在平面直角坐标系中点P（-2，3）和Q（m，n）关于x轴对称，则m的值为（ ）
| A． | m=-2 | B． | m=2 | C． | m=-3 | D． | m=3 |