题目内容
2.下列运算正确的是( )| A. | ($\sqrt{4}$)2=4 | B. | $\sqrt{(-4)^{2}}$=-4 | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ |
分析 分别利用二次根式的性质以及结合二次根式混合运算法则化简求出答案.
解答 解:A、($\sqrt{4}$)2=4,正确;
B、$\sqrt{(-4)^{2}}$=4,故此选项错误;
C、$\sqrt{(-4)×(-9)}$=$\sqrt{4}$×$\sqrt{9}$,故此选项错误;
D、$\sqrt{7}$-$\sqrt{5}$无法计算,故此选项错误;
故选:A.
点评 此题主要考查了二次根式的混合运算以及二次根式的化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
1.小雪在作业本上做了四道题目:①$\root{3}{-27}$=-3;②±$\sqrt{16}$=4;③$\root{3}{81}$=9;④$\sqrt{(-6)^{2}}$=6,她做对了的题目有( )
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
10.下列因式分解正确的是( )
| A. | 4m2-4m+1=4m(m-1) | B. | a3b2-a2b+a2=a2(ab2-b) | ||
| C. | x2-7x-10=(x-2)(x-5) | D. | 10x2y-5xy2=5xy(2x-y) |
7.若-1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果是( )
| A. | -3 | B. | 3 | C. | -2x+1 | D. | 2x-1 |
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.已知am=9,am-n=3,则an的值是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | 1 |
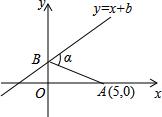 如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$. 如图,AB∥ED,∠B+∠C+∠D=360°.
如图,AB∥ED,∠B+∠C+∠D=360°.