题目内容
20.已知△ABC中,O是三角形内一点,满足∠BAO=∠CAO=∠CBO=∠ACO,求证:BC2=AC•AB.分析 根据已知条件∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}∠$BAC,得到OA=OC,设∠BAC=α,∠ABC=β,∠ACB=γ,由正弦定理得$\frac{OA}{sin(β-\frac{1}{2}α)}$=$\frac{BO}{sin\frac{1}{2}α}$,$\frac{CO}{sin\frac{1}{2}α}$=$\frac{BO}{sin(γ-\frac{1}{2}α)}$,两式相比得到sin2$\frac{1}{2}α$=sin($β-\frac{1}{2}α$)•sin(γ-$\frac{1}{2}α$),化简后即可得到结论.
解答 解:∵∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}∠$BAC,
∴OA=OC,
设∠BAC=α,∠ABC=β,∠ACB=γ,
在△ABO和△BCO中,由正弦定理得$\frac{OA}{sin(β-\frac{1}{2}α)}$=$\frac{BO}{sin\frac{1}{2}α}$,$\frac{CO}{sin\frac{1}{2}α}$=$\frac{BO}{sin(γ-\frac{1}{2}α)}$,
∵AO=CO,
∴两式相比得:sin2$\frac{1}{2}α$=sin($β-\frac{1}{2}α$)•sin(γ-$\frac{1}{2}α$),
∴1-cosα=cos(β-γ)-cos(β+γ-α),1+cos(β+γ-α)=cos(β-γ)+cosα.
∵β+γ-α=180°-2α,
∴2sin2α=2sinβsinγ,
∴BC2=AC•AB.
点评 本题考查了三角形的内角和,正弦定理,三角函数,正确掌握正弦定理是解题的关键.

练习册系列答案
相关题目
14.计算$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}y+x{y}^{2}}$$•\frac{xy}{x-y}$的结果为( )
| A. | $\frac{x-y}{x+y}$ | B. | $\frac{x+y}{x-y}$ | C. | $\frac{(x-y)^{2}}{x+y}$ | D. | 1 |
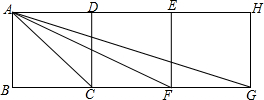 如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG
如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG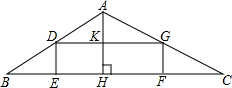 如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16.
如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16.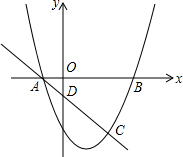 抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).
抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).