题目内容
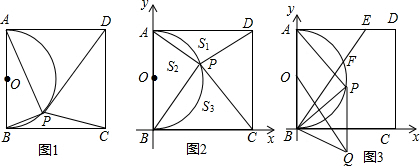
 如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第
如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第考点:圆周角定理
专题:
分析:首先连接OE,根据直角所对的弦是直径,可得点C在以O圆心,AB为直径的圆上,然后由圆周角定理,可得∠ACP=
∠AOE,则可求得∠ACP的度数,继而求得答案.
| 1 |
| 2 |
解答: 解:连接OE,
解:连接OE,
∵∠ACB=90°,
∴点C在以O圆心,AB为直径的圆上,
∴∠ACP=
∠AOE,
∵∠AOE=120°,
∴∠ACP=60°,
∵射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,
∴60÷2=30(s),
∴第30秒时,点E在量角器上对应的读数是120度.
故答案为:30.
 解:连接OE,
解:连接OE,∵∠ACB=90°,
∴点C在以O圆心,AB为直径的圆上,
∴∠ACP=
| 1 |
| 2 |
∵∠AOE=120°,
∴∠ACP=60°,
∵射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,
∴60÷2=30(s),
∴第30秒时,点E在量角器上对应的读数是120度.
故答案为:30.
点评:此题考查了圆周角定理以及旋转的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )
如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )| A、4cm | ||
B、2
| ||
C、2
| ||
D、
|
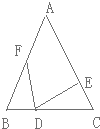 如图,在△ABC中,AB=AC,D为BC上一点,且BD=CE,∠BFD=∠CDE.
如图,在△ABC中,AB=AC,D为BC上一点,且BD=CE,∠BFD=∠CDE.
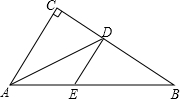 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.