题目内容
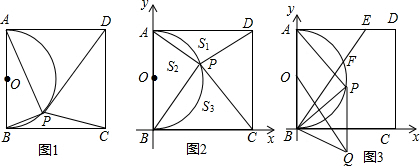
已知四边形ABCD是边长为2的正方形,在以AB为直径的正方形内作半圆O,P为半圆上的动点(不与A、B重合)连接PA、PB、PC、PD,
(1)若DP与半圆O相切时,求PA的长.
(2)如图,以BC边为x轴,以AB边为y轴,建立如图所示的平面直角坐标系,把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3,试求2S1S3-S22的最大值,并求出此时点P的坐标.
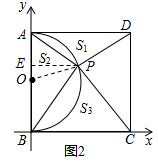
(3)在(2)的条件下,E为边AD上一点,且AE=3DE,连接BE交半圆O于F.连接FP并延长至点Q,使得PQ=PB,求OQ的长.
(1)若DP与半圆O相切时,求PA的长.
(2)如图,以BC边为x轴,以AB边为y轴,建立如图所示的平面直角坐标系,把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3,试求2S1S3-S22的最大值,并求出此时点P的坐标.
(3)在(2)的条件下,E为边AD上一点,且AE=3DE,连接BE交半圆O于F.连接FP并延长至点Q,使得PQ=PB,求OQ的长.

考点:圆的综合题
专题:压轴题
分析:(1)根据已知可得OD垂直平分AP,得到△AMO∽△DAO,根据勾股定理从而得到AM,即可得到AP的值;
(2)过点P分别作PE⊥AB,设P点坐标为(x,y),通过勾股定理得到x2=2y-y2,从而得到2S1S3-S22关于x的解析式,求得其最值即可得到P的坐标;
(3)连接AF,作FK⊥AB交于点K,易得△BAE∽△BFA∽△AFE,根据相似三角形的性质得到BF,从而根据勾股定理以及△BFK∽△BEA,得到BE、FK及BK,即可得出F点坐标,接着得到直线PF解析式,设Q(a,-7a+8),利用PQ=PB=
得到Q点坐标,即可得到OQ的长度.
(2)过点P分别作PE⊥AB,设P点坐标为(x,y),通过勾股定理得到x2=2y-y2,从而得到2S1S3-S22关于x的解析式,求得其最值即可得到P的坐标;
(3)连接AF,作FK⊥AB交于点K,易得△BAE∽△BFA∽△AFE,根据相似三角形的性质得到BF,从而根据勾股定理以及△BFK∽△BEA,得到BE、FK及BK,即可得出F点坐标,接着得到直线PF解析式,设Q(a,-7a+8),利用PQ=PB=
| 2 |
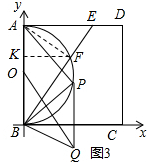
解答: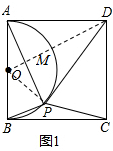 解:(1)如图1,连接OP、OD,AP与OD相交于点M,
解:(1)如图1,连接OP、OD,AP与OD相交于点M,
∵DP与半圆O相切,
∴OA=OP,OP⊥DP,得OD垂直平分AP,
∴△AMO∽△DAO,
∴
=
,
∵AD=2,AO=1,
DO=
=
=
,
∴AM=
=
=
,
∴AP=2AM=2×
=
;
(2)作PE⊥AB于点E,设P(x,y),
在Rt△EPO中,可得PE2+EO2=OP2,
即x2+(y-1)2=12,
∴x2=2y-y2,
根据题意可得:S1=
•AD•(2-y)=2-y,
S3=
•BC•y=y,
S2=
•AB•x=x,
∴2S1S3-S22=2•(2-y)•y-x2
=4y-2y2-x2
=x2
∵0<x≤1
∴当x=1时,2S1S3-S22有最大值,最大值为1,
将x=1代入x2=2y-y2中,
可得y=1,
此时点P(1,1)
(3)连接AF,得AF⊥BE,作FK⊥AB交于点K,
∵AE=3DE,AD=2,
∴AE=
,AF=
,
根据题意,易得△BAE∽△BFA∽△AFE,
即:
=
=
,
得BF=
=
=
,
在△ABE中,BE=
=
,
易得△BFK∽△BEA,
即:
=
,
得FK=
•BF=
=
,
根据勾股定理可得,BK=
=
∴F(
,
),
∵P(1,1),
可求得直线PF解析式:y=-7x+8,
设Q(a,-7a+8),
∵PQ=PB=
,
∴
=
,
∴a1=
,a2=
,
∵Q在FP的延长上,
∴a>1,
∴a=
,
∴Q点坐标为(
,-
),
∵O点坐标为(0,1),
∴QO=
=
.
 解:(1)如图1,连接OP、OD,AP与OD相交于点M,
解:(1)如图1,连接OP、OD,AP与OD相交于点M,∵DP与半圆O相切,
∴OA=OP,OP⊥DP,得OD垂直平分AP,
∴△AMO∽△DAO,
∴
| AM |
| AD |
| AO |
| DO |
∵AD=2,AO=1,
DO=
| AD2+AO2 |
| 22+12 |
| 5 |
∴AM=
| AO×AD |
| DO |
| 1×2 | ||
|
2
| ||
| 5 |

∴AP=2AM=2×
2
| ||
| 5 |
4
| ||
| 5 |
(2)作PE⊥AB于点E,设P(x,y),
在Rt△EPO中,可得PE2+EO2=OP2,
即x2+(y-1)2=12,
∴x2=2y-y2,
根据题意可得:S1=
| 1 |
| 2 |
S3=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
∴2S1S3-S22=2•(2-y)•y-x2
=4y-2y2-x2
=x2
∵0<x≤1
∴当x=1时,2S1S3-S22有最大值,最大值为1,
将x=1代入x2=2y-y2中,
可得y=1,
此时点P(1,1)
(3)连接AF,得AF⊥BE,作FK⊥AB交于点K,
∵AE=3DE,AD=2,
∴AE=
| 3 |
| 2 |
| 6 |
| 5 |

根据题意,易得△BAE∽△BFA∽△AFE,
即:
| AF |
| BF |
| EF |
| AF |
| AE |
| AB |
得BF=
| AF•AB |
| AE |
| ||
|
| 8 |
| 5 |
在△ABE中,BE=
| AB2+AE2 |
| 5 |
| 2 |
易得△BFK∽△BEA,
即:
| FK |
| BF |
| AE |
| BE |
得FK=
| AE |
| BE |
| ||||
|
| 24 |
| 25 |
根据勾股定理可得,BK=
| BF2-FK2 |
| 32 |
| 25 |
∴F(
| 24 |
| 25 |
| 32 |
| 25 |
∵P(1,1),
可求得直线PF解析式:y=-7x+8,
设Q(a,-7a+8),
∵PQ=PB=
| 2 |
∴
| (a-1)2+(-7a+8-1)2 |
| 2 |
∴a1=
| 4 |
| 5 |
| 6 |
| 5 |
∵Q在FP的延长上,
∴a>1,
∴a=
| 6 |
| 5 |
∴Q点坐标为(
| 6 |
| 5 |
| 2 |
| 5 |
∵O点坐标为(0,1),
∴QO=
(
|
| ||
| 5 |
点评:本题考查了圆的综合题,涉及了相似三角形的判定与性质、勾股定理、二元一次方程的最值问题、两点间的距离等多个考点,此题综合性很强,解题的关键是在于数形结合与方程思想的变换,特别是第(3)问中计算量较大,需要仔细认真.

练习册系列答案
相关题目
 如图,AB是⊙O的切线,点B为切点,BC是⊙O的直径,∠A=20°,则∠ODC的度数为( )
如图,AB是⊙O的切线,点B为切点,BC是⊙O的直径,∠A=20°,则∠ODC的度数为( )| A、70° | B、60° |
| C、55° | D、40° |
在分别标有号码2、3、4、…10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第
如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第 已知△ABC,
已知△ABC,