题目内容
如图，Rt△ABC中，∠C=90°，D为CA上一点，∠DBC=30°，DA=3，AB=
，试求cosA与tanA的值．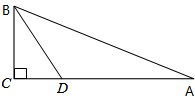
| 19 |
考点：解直角三角形,勾股定理
专题：计算题
分析：在直角三角形BCD中，利用30度角所对的直角边等于斜边的一半得到BD=2CD，设CD=x，则有BD=2x，利用勾股定理表示出BC，由CD+AD表示出AC，在直角三角形ABC中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出BC与AC的长，即可求出tanA与cosA的值．
解答：解：在Rt△BCD中，∠C=90°，∠DBC=30°，
设CD=x，则有BD=2x，
根据勾股定理得：BC=
x，
∵DA=3，AB=
，
∴在Rt△ABC中，BC=
x，AC=CD+AD=x+3，
根据勾股定理得：BC2+AC2=AB2，即3x2+（x+3）2=19，
整理得：2x2+3x-5=0，即（2x+5）（x-1）=0，
解得：x=1（负值舍去），
∴BC=
，AC=4，
则cosA=
=
=
，tanA=
=
．
设CD=x，则有BD=2x，
根据勾股定理得：BC=
| 3 |
∵DA=3，AB=
| 19 |
∴在Rt△ABC中，BC=
| 3 |
根据勾股定理得：BC2+AC2=AB2，即3x2+（x+3）2=19，
整理得：2x2+3x-5=0，即（2x+5）（x-1）=0，
解得：x=1（负值舍去），
∴BC=
| 3 |
则cosA=
| AC |
| AB |
| 4 | ||
|
4
| ||
| 19 |
| BC |
| AC |
| ||
| 4 |
点评：此题属于解直角三角形题型，涉及的知识有：勾股定理，锐角三角函数定义，以及含30度直角三角形的性质，熟练掌握勾股定理及性质是解本题的关键．
练习册系列答案
相关题目
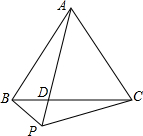如图所示，点P是等边△ABC外一点，∠APC=60°，PA、BC交于点D，求证：PA=PB+PC．
如图，量角器的直径与直角三角板△ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转（旋转时间不超过45秒），CP与量角器的半圆弧交于点E，第