题目内容
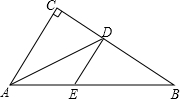 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.考点:勾股定理,角平分线的性质,平行线分线段成比例
专题:
分析:利用已知条件易证AE=DE,因为DE∥AC,所以可得到BE和AE的关系,即BE和DE的关系,设AE=4x,根据勾股定理可得BE2=DE2+BD2,求出x的值,进而得到AE,BE的长.
解答:解:∵AD平分∠BAC,
∴∠CAD=∠DAE,
∵DE∥CA,
∴∠DAE=∠ADE,
∴AE=DE,
∵DE∥CA,
∴AE:BE=CD:BD=12:15=4:5,
设AE=4x
则DE=4x,BE=5x,
∵AC⊥BC,DE∥CA,
∴DE⊥BD,
由勾股定理得BE2=DE2+BD2,
所以25x2=16x2+225,
解得x=5,
∴AE=4×5=20,BE=5×5=25.
∴∠CAD=∠DAE,
∵DE∥CA,
∴∠DAE=∠ADE,
∴AE=DE,
∵DE∥CA,
∴AE:BE=CD:BD=12:15=4:5,
设AE=4x
则DE=4x,BE=5x,
∵AC⊥BC,DE∥CA,
∴DE⊥BD,
由勾股定理得BE2=DE2+BD2,
所以25x2=16x2+225,
解得x=5,
∴AE=4×5=20,BE=5×5=25.
点评:本题考查了等腰三角形的判定和性质、平行线的性质以及勾股定理的运用,解题的关键是利用平行线分线段成比例定理得到AE和BE的数量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,直线y=
如图,直线y= 如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第
如图,量角器的直径与直角三角板△ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转(旋转时间不超过45秒),CP与量角器的半圆弧交于点E,第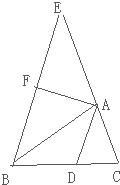
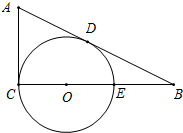 在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.
在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.