题目内容
2.在△ABC中,AB=BC=AC=6,则△ABC的面积为( )| A. | 9 | B. | 18 | C. | 9$\sqrt{3}$ | D. | 18$\sqrt{3}$ |
分析 根据等边三角形三线合一的性质,可求得D为BC中点且AD⊥BC,根据勾股定理即可求AD的值,根据AD、BC即可计算△ABC的面积.
解答 解:如图,作AD⊥BC于D,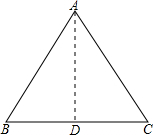
∵AB=BC=AC=6,
∵AD为BC边上的高,则D为BC的中点,
∴BD=DC=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=3\sqrt{3}$,
∴等边△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$.
故选C.
点评 本题考查了等边三角形三线合一的性质,考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,本题中根据勾股定理计算AD的长是解题的关键.

练习册系列答案
相关题目
7.某数的平方根为2a+3与a-15,这个数是( )
| A. | 121 | B. | 11 | C. | ±11 | D. | 4 |
14.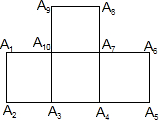 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.| A. | 18 | B. | 22 | C. | 24 | D. | 26 |
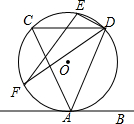 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
 如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.
如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.