题目内容
9.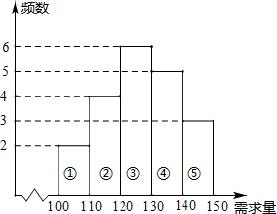 经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.
经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.完成下列问题:
(1)根据直方图可以看出,销售月内市场需求量的中位数在第③组.
(2)当100≤x≤150时,用含x的代数式或常数表示T;
(3)根据直方图估计利润T不少于57000元的概率.
分析 (1)根据中位数定义,20个数据中位数取第10、11个数据的平均数;
(2)分两种情况:100≤x<130、130≤x≤150分别根据利润=毛利润-因产品未售出亏损总费用、总利润=单件利润×销售量,列函数关系式;
(3)由(2)可求得利润不少于57000元时x的范围,结合直方图可确定在此范围内的频数,进而求得频率即概率.
解答 解:(1)一共20个数据,中位数是第10、11个数据的平均数,
由图可知第10、11个数据均落在第③组,
故销售月内市场需求量的中位数在第③组;
(2)当100≤x<130时,T=500x-300(130-x)=800x-39000;
当130≤x≤150时,T=500×130=65000;
(3)由题意可知,800x-39000≥57000,
解得:x≥120,
所以当120≤x≤150时,利润不少于57000元,
根据直方图估计月内市场需求量120≤x≤150的频数为6+5+3=14,
则估计月内市场需求量120≤x≤150的频率为14÷20=0.7,
所以估计利润不小于57000元的概率为0.7.
故答案为:(1)③.
点评 本题主要考查频数(率)分布直方图的应用及函数解析式求法、频率估计概率等,解题时注意频(数)率分布直方图的合理运用.

练习册系列答案
相关题目
4.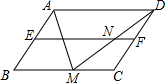 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
14.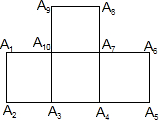 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
 如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.
如图,在四个正方形拼接成的图形中,以这十个点中任意三点为顶点,共能组成( )个等腰直角三角形.| A. | 18 | B. | 22 | C. | 24 | D. | 26 |
 如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.
如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.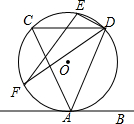 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$. 如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.
如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.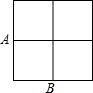 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.