题目内容
17. 如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2.
如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2.
分析 首先由等腰三角形的性质可知BD=DC,从而可知AD是图形的对称轴,由轴对称图形的性质可知:阴影部分的面积等于△ABC面积的一半.
解答 解:∵AB=AC,AD是BC边上的高线,
∴BD=DC.
∵BD=DC,AD⊥BC,
∴AD是△ABC的对称轴.
由轴对称图形的性质可知:△EFC的面积=△BEF的面积.
∴阴影部分的面积=$\frac{1}{2}$△ABC的面积=6cm2.
故答案为:6.
点评 本题主要考查的是等腰三角形的性质、轴对称的性质,利用轴对称的性质得到阴影部分的面积=$\frac{1}{2}$S△ABC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列调查中,最适宜采用全面调查方式(普查)的是( )
| A. | 对益阳市小学生每天学习所用时间的调查 | |
| B. | 对全国中学生心理健康现状的调查 | |
| C. | 对某班学生进行6月5日是“世界环境日”知晓情况的调查 | |
| D. | 对益阳市初中学生课外阅读量的调查 |
6.a与-2互为相反数,那么a是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
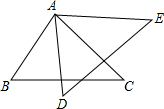 如图,已知△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠DAC=40°.
如图,已知△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠DAC=40°.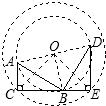 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π)
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π)