题目内容
7.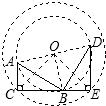 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π)
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π)
分析 Rt△ABC绕O点旋转90°得Rt△BDE,C、E两点为对应点,由旋转的性质可知,OC=OE,∠COE=90°,AC与BE,BC与DE对应,故有CE=BE+BC=AC+DE=8,再由勾股定理求OC;Rt△ABC绕C点旋转一周,则线段AB扫过的面积是以C为圆心CB为半径的圆的面积-以C为圆心CA为半径的圆的面积,据此可得.
解答 解:由旋转的性质可知,OC=OE,∠COE=90°,
∵AC与BE,BC与DE对应,
∴CE=BE+BC=AC+DE=8,
∴由勾股定理得,OC2+OE2=CE2,
即2OC2=64,解得OC=4$\sqrt{2}$;
若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是π•CB2-π•CA2=25π-9π=16π,
故答案为:4$\sqrt{2}$,16π.
点评 本题主要考查旋转的性质、勾股定理及扇形的面积公式,熟练掌握旋转的性质及Rt△ABC绕C点旋转一周,线段AB扫过图形的构成是解题的关键.

练习册系列答案
相关题目
15.2016年底,我国人口总数约13.85亿左右,这个数据用科学记数法表示为( )
| A. | 1.385×102人 | B. | 13.85×108人 | C. | 1.385×109人 | D. | 1.385×108人 |
12.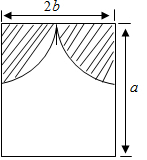 长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
 长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )| A. | 2a2-πb2 | B. | 2a2-$\frac{π}{2}$b2 | C. | 2ab-$\frac{π}{2}$b2 | D. | 2ab-πb2 |
19.已知a是一元二次方程x2-x-1=0的根,则2016-a+a2的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 0 |
 如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2.
如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2. 如图,矩形ABCD中,线段EF过对角线的交点O,交AB、CD于点E、F,阴影部分的面积为S1,矩形ABCD的面积为S,则$\frac{{S}_{1}}{S}$=$\frac{1}{4}$.
如图,矩形ABCD中,线段EF过对角线的交点O,交AB、CD于点E、F,阴影部分的面积为S1,矩形ABCD的面积为S,则$\frac{{S}_{1}}{S}$=$\frac{1}{4}$.