题目内容
1．角平分线上的任意一点到这个角的两边的距离相等；线段垂直平分线上的点到线段两端点的距离相等；线段的垂直平分线可以看作是到线段两端点距离相等的所有点的集合；角平分线可以看作是到角两边距离相等的所有点的集合．分析 分别根据角平分线及线段垂直平分线的性质、线段的定义进行解答即可．
解答 解：角平分线上的任意一点到这个角的两边的距离相等；线段垂直平分线上的点到 线段两端点的距离相等；线段的垂直平分线可以看作是到 线段两端点距离相等的所有点的集合；角平分线可以看作是到角两边距离相等的所有点的集合．
故答案为：距离；线段两端点；线段两端点距离相等；角两边距离相等．
点评 本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
已知a，b表示有理数，在数轴上用点表示如图所示，且|a|＞1＞|b|，请完成下列各题：
16．
如图所示，在A处观察C，得仰角∠CAD=31°，且A、B的水平距离AE=800米，AB的坡度i=1：2，索道BC的坡度i=2：3，CD⊥AD于D，BF⊥CD于F．则索道BC的长大约是（ ）（参考数据：tan31°≈0.6，cos31°≈0.9，$\sqrt{13}$≈3.6）
如图所示，在A处观察C，得仰角∠CAD=31°，且A、B的水平距离AE=800米，AB的坡度i=1：2，索道BC的坡度i=2：3，CD⊥AD于D，BF⊥CD于F．则索道BC的长大约是（ ）（参考数据：tan31°≈0.6，cos31°≈0.9，$\sqrt{13}$≈3.6）| A． | 1400 | B． | 1440 | C． | 1500 | D． | 1540 |
6．
观察如图一组数：-1，2，-3，4，-5，6，-7，…．，将这组数排成如图的形式，按照如图规律排下去，则第10行中从左边数第10个数是（ ）
观察如图一组数：-1，2，-3，4，-5，6，-7，…．，将这组数排成如图的形式，按照如图规律排下去，则第10行中从左边数第10个数是（ ）| A． | -90 | B． | 90 | C． | -91 | D． | 91 |
13．
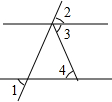如图，已知∠1=∠2，∠3=65°，则∠4=（ ）
如图，已知∠1=∠2，∠3=65°，则∠4=（ ）| A． | 115° | B． | 55° | C． | 25° | D． | 65° |
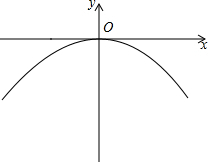有一座抛物线形拱桥，正常水位时，桥下水面宽20m，拱顶距离水面4m．