题目内容
6. 观察如图一组数:-1,2,-3,4,-5,6,-7,….,将这组数排成如图的形式,按照如图规律排下去,则第10行中从左边数第10个数是( )
观察如图一组数:-1,2,-3,4,-5,6,-7,….,将这组数排成如图的形式,按照如图规律排下去,则第10行中从左边数第10个数是( )| A. | -90 | B. | 90 | C. | -91 | D. | 91 |
分析 根据数的变化找出奇数为负偶数为正,再根据数的排列找出第n行有2n-1个数,求出前九行的数的个数+10即可得出第10行中从左边数第10个数的绝对值,根据其奇偶性即可得出结论.
解答 解:观察数列可知,奇数为负偶数为正,
观察图形可知:第一行1个数,第二行3个数,第三行5个数,第四行7个数,
∴第n行有2n-1个数,
∴前九行共有:1+3+5+…+17=$\frac{9×(1+17)}{2}$=81,
∴81+10=91,
∴第10行中从左边数第10个数是-91.
故选C.
点评 本题考查了规律型中得数字的变化类,解题的关键是根据数的排列找出第n行有2n-1个数.本题属于基础题,难度不大,解决该题型题目时,根据数值的变化找出变化规律是关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a2=a4 | C. | (-a3)2=a6 | D. | (a2b)2=a4b |
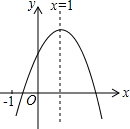 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论: