题目内容
12. 已知a,b表示有理数,在数轴上用点表示如图所示,且|a|>1>|b|,请完成下列各题:
已知a,b表示有理数,在数轴上用点表示如图所示,且|a|>1>|b|,请完成下列各题:①|a|=-a,②|b|=b,③a+b<,④a+(-b)<0,⑤-a+b>0,⑥-a(-b)<0.
分析 根据a、b两点在数轴上的位置判断出其取值范围,再对各选项进行逐一分析即可.
解答 解:因为a<-1<0<b<1,
所以①|a|=-a,②|b|=b,③a+b<0,④a+(-b)<0,⑤-a+b>0,⑥-a(-b)<0.
故答案为:-a;b;<;<;>;<
点评 本题考查的是数轴的特点,根据a、b两点在数轴上的位置判断出其取值范围是解答此题的关键.

练习册系列答案
相关题目
2.计算22008+(-2)2009的结果是( )
| A. | 2 | B. | -2 | C. | -22008 | D. | 22008 |
7.下列方程中,是二次方程的是( )
| A. | x2+2=0 | B. | x3+2x=0 | C. | x4+2x3+1=0 | D. | $\frac{1}{{x}^{2}}$+5=0 |
17.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a2=a4 | C. | (-a3)2=a6 | D. | (a2b)2=a4b |
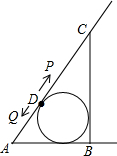 如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.
如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.