题目内容
4.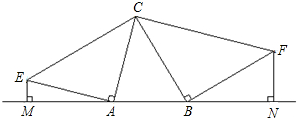 如图,锐角△ABC分别以A、B为直角顶点,向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF,再分别过点E、F作边AB所在直线的垂线,垂足为M,N.
如图,锐角△ABC分别以A、B为直角顶点,向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF,再分别过点E、F作边AB所在直线的垂线,垂足为M,N.求证:EM+FN=AB.
分析 过C作CG垂直于AB,由EA垂直于AC,利用平角的定义得到一对角互余,再由CG垂直于AG,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等及AE=AC,利用AAS得到三角形ACG与三角形AEM全等,利用全等三角形的对应边相等得到EM=AG,同理得到BG=FN,由AB=AG+GB,等量代换即可得证.
解答 解:如图,过C作CG⊥AB,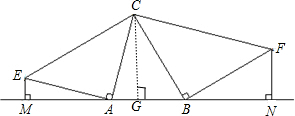
∴∠CAG+∠ACG=90°,
∵△AEC为等腰直角三角形,
∴∠EAC=90°,AE=AC,
∴∠CAG+∠EAM=90°,
∴∠ACG=∠EAM,
∵在△ACG和△EAM中,
$\left\{\begin{array}{l}{∠AGC=∠EMA}\\{∠ACG=∠EAM}\\{AC=AE}\end{array}\right.$,
∴△ACG≌△EAM(AAS),
∴EM=AG,
同理GB=FN,
∴AB=AG+GB=EM+FN.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,圆周角定理,轴对称-最短线路问题,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
14.计算:$\frac{4}{{x}^{2}-4}$-$\frac{1}{x-2}$的正确结果是( )
| A. | -$\frac{1}{x+2}$ | B. | 1-x | C. | 1 | D. | -1 |
6.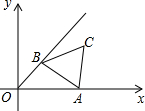 如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
 如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{3}$ | D. | 1+2$\sqrt{2}$ |
 如图1,直线AB∥CD,P是截线MN上的一点.
如图1,直线AB∥CD,P是截线MN上的一点.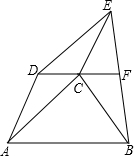 已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.
已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.


