题目内容
16. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( )
如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( )| A. | 2.5 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{10}$-1 |
分析 先利用勾股定理求出AC,根据AC=AM,求出OM,由此即可解决问题,
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=3,AD=BC=1,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵AM=AC=$\sqrt{10}$,OA=1,
∴OM=$\sqrt{10}$-1,
∴点M表示点数为$\sqrt{10}$-1.
故选D.
点评 本题考查实数与数轴、勾股定理等知识,解题的关键是灵活应用勾股定理求出AC、AM的长,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
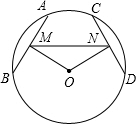 如图,AB、CD是⊙O的弦,OM⊥AB,ON⊥CD,垂足分别为M、N,且∠AMN=∠CNM.
如图,AB、CD是⊙O的弦,OM⊥AB,ON⊥CD,垂足分别为M、N,且∠AMN=∠CNM. 平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.
平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D. 已知:如图,AB=AC,AD=AE.
已知:如图,AB=AC,AD=AE.