题目内容
已知△ABC中,AD是BC上的中线,AD⊥AB,如果AC=5,AD=2,那么AB的长?画出这张图.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:先根据题意画出图形,延长AD到E,使AD=DE,连接CE,正出△ADB≌△EDC,推出AB=CE,∠E=∠BAD=90°,AD=DE=2,在Rt△AEC中,由勾股定理求出CE即可.
解答:解:如图:

∵AD⊥AB,
∴∠BAD=90°,
如图,延长AD到E,使AD=DE,连接CE,

∵AD为中线,
∴BD=DC,
在△ADB和△EDC中,
,
∴△ADB≌△EDC(SAS),
∴AB=CE,∠E=∠BAD=90°,AD=DE=2,
在Rt△AEC中,由勾股定理得:AB=CE=
=3.

∵AD⊥AB,
∴∠BAD=90°,
如图,延长AD到E,使AD=DE,连接CE,

∵AD为中线,
∴BD=DC,
在△ADB和△EDC中,
|
∴△ADB≌△EDC(SAS),
∴AB=CE,∠E=∠BAD=90°,AD=DE=2,
在Rt△AEC中,由勾股定理得:AB=CE=
| 52-(2+2)2 |
点评:本题考查了全等三角形的性质和判定,勾股定理的应用,能正确作出辅助线并能求出△AEC是直角三角形运用全等三角形的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
圆绕着某一点旋转任意角度都能与自身重合,这一点是( )
| A、圆心 | B、点O |
| C、圆内任意一点 | D、圆上任意一点 |

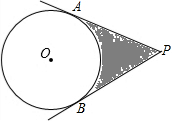 如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长. 如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?
如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?