题目内容
已知如图所示,PA=PB,∠1+∠2=180°,求证:OP平分∠AOB.


考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:求出∠1=∠PBN,过P作PM⊥OA于M,PN⊥OB于N,证△PMA≌△PNB,推出PM=PN,根据角平分线性质得出即可.
解答:证明:∵∠2+∠PBN=180°,∠1+∠2=180°,
∴∠1=∠PBN,
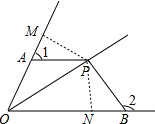 过P作PM⊥OA于M,PN⊥OB于N,
过P作PM⊥OA于M,PN⊥OB于N,
则∠PMA=∠PNB=90°,
在△PMA和△PNB中,
,
∴△PMA≌△PNB(AAS),
∴PM=PN,
∵PM⊥OA,PN⊥OB,
∴OP平分∠AOB.
∴∠1=∠PBN,
 过P作PM⊥OA于M,PN⊥OB于N,
过P作PM⊥OA于M,PN⊥OB于N,则∠PMA=∠PNB=90°,
在△PMA和△PNB中,
|
∴△PMA≌△PNB(AAS),
∴PM=PN,
∵PM⊥OA,PN⊥OB,
∴OP平分∠AOB.
点评:本题考查了全等三角形的性质和判定,角平分线的性质的应用,正确作出辅助线后推出△PMA≌△PNB是解此题的关键.

练习册系列答案
相关题目
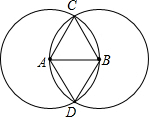 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
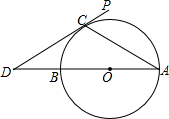 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )| A、30° | B、32° |
| C、34° | D、36° |