题目内容
4.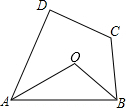 如图,在四边形ABCD中,AO平分∠DAB,BO平分∠ABC,且∠D+∠C=220°.求∠AOB的度数.
如图,在四边形ABCD中,AO平分∠DAB,BO平分∠ABC,且∠D+∠C=220°.求∠AOB的度数.
分析 根据三角形内角和等于180°,四边形内角和等于360°,结合角平分线的定义即可得到∠AOB与∠C+∠D之间的关系.
解答 证明:∵AO平分∠DAB,BO平分∠ABC,
∴∠OAB=$\frac{1}{2}$∠DAB,∠OBA=$\frac{1}{2}$∠ABC,
∴∠AOB=180°-(∠OAB+∠OBA)
=180°-$\frac{1}{2}$(∠DAB+∠CBA)
=180°-$\frac{1}{2}$(360°-∠C-∠D)
=$\frac{1}{2}$(∠C+∠D),
∵∠C+∠D=220°,
∴∠AOB=$\frac{1}{2}$(∠C+∠D)=110°.
点评 本题考查了角平分线的定义,多边形内角和定理,关键是熟悉三角形内角和等于180°,四边形内角和等于360°.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
16.某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
| A 组 | -1.5 | +1.5 | -1 | -2 | -2 |
| B组 | +1 | +3 | -3 | +2 | -3 |
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
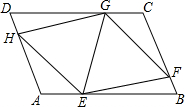 如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.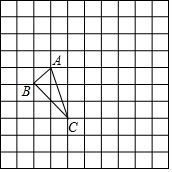 如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.