题目内容
4.已知x+y=-7,x2+y2=29,求xy与x-y的值.分析 先根据完全平方公式求出2xy的值,求出xy,再根据完全平方公式变形,即可求出x-y的值.
解答 解:∵x+y=-7,
∴(x+y)2=49,
∴x2+2xy+y2=49,
∵x2+y2=29,
∴2xy=49-29=20,
∴xy=10,
∴x-y
=$±\sqrt{(x-y)^{2}}$
=±$\sqrt{(x+y)^{2}-4xy}$
=±$\sqrt{(-7)^{2}-4×10}$
=±3.
点评 本题考查了完全平方公式,能正确根据完全平方公式进行变形是解此题的关键.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线相交所成的四个角相等,则这两条直线互相垂直 | |
| D. | 相等的两个角是对顶角 |




 如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.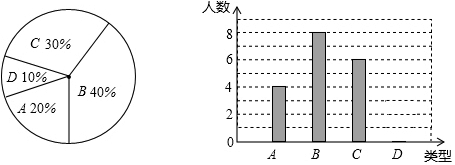
 用描点法作出函数y=2x+4的图象,
用描点法作出函数y=2x+4的图象,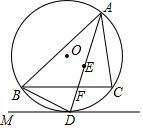 如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.
如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.