题目内容
15. 如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.(1)若∠ABC=42°,∠ACB=48°,则∠BOC=135°.
(2)若∠A=70°,则∠BOC=125°.
(3)若∠A=120°,则∠BOC=150°.
(4)若∠A=α°,请猜想∠BOC的度数,并说明理由.
分析 (1)先根据角平分线的性质得出∠OBC与∠OCB的度数,再根据三角形内角和定理即可得出结论;
(2)先根据∠A=40°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论;
(3)先根据∠A=120°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论;
(4)根据∠A=x°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论.
解答 解:(1)∵在△ABC中,∠ABC=42°,∠ACB=48°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×42°=21°,∠OCB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×48°=24°,
∴∠BOC=180°-∠OBC-∠OCB=180°-21°-24°=135°;
故答案是:135°;
(2)∵在△ABC中,∠A=70°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-70°)=55°,
∴∠BOC=180°-55°=125°;
故答案是:125°;
(3)∵在△ABC中,∠A=120°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-120°)=30°,
∴∠BOC=180°-30°=150°;
故答案是:150°;
(4)在△ABC中,∠A=x°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-x°)=90°-$\frac{1}{2}$x°,
∴∠BOC=180°-(90°-x°)=90°+$\frac{1}{2}$x°
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

| A. | M | B. | C | C. | N | D. | I |
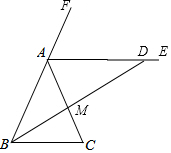 已知:如图,AE平分△ABC的一个外角∠CAF,且AE∥BC.
已知:如图,AE平分△ABC的一个外角∠CAF,且AE∥BC.