题目内容
9. 用描点法作出函数y=2x+4的图象,
用描点法作出函数y=2x+4的图象,步骤1、列表;
步骤2、描点;
步骤3、连线.
并根据图象回答:
(1)直线y=2x+4经过点A(-1,2)(填“经过”或“不经过”);
(2)当x<-2时,y<0.
分析 列表、描点、连线画出函数图象.
(1)将x=-1代入一次函数解析式中求出y轴,将其与x进行比较后可得出直线y=2x+4经过点A(-1,2);
(2)观察函数图象,根据直线与x轴的上下位置关系,即可得出结论.
解答 解:步骤1、列表.
| x | 0 | -2 |
| y | 4 | 0 |

步骤3、连线.
(1)当x=-1时,y=2x+4=2,
∴直线y=2x+4经过点A(-1,2).
(2)观察函数图象,可知:当x<-2时,直线在x轴下方,
∴当x<-2时,y<0.
故答案为:(1)经过;(2)<-2.
点评 本题考查了一次函数的图象以及一次函数图象上点的坐标特征,解题的关键是:(1)利用一次函数图象上点的坐标特征求出当x=-1时的y值;(2)由直线与x轴的上下位置关系,找出y<0时x的取值范围.

练习册系列答案
相关题目
14. 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE平分∠AOB | B. | 点C、D到OE的距离不一定相等 | ||
| C. | OC=OD | D. | 点E到OA、OB的距离一定相等 |
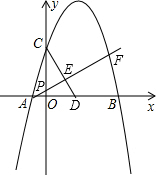 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,且OB=OC=3OA,点P为线段OC上一动点,射线AP与抛物线交于点F,CD⊥AF于点E,交x轴于点D.
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,且OB=OC=3OA,点P为线段OC上一动点,射线AP与抛物线交于点F,CD⊥AF于点E,交x轴于点D.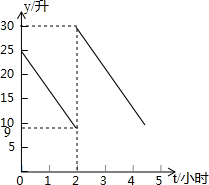 张师傅驾车从甲地到乙地,两地相距S千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以同样的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.张师傅途中加油21升.
张师傅驾车从甲地到乙地,两地相距S千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以同样的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.张师傅途中加油21升.