题目内容
14.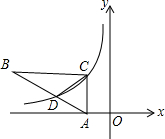 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
分析 作BE⊥x轴于E,DF⊥x轴于F,设OA=a,AE=b,用a、b表示出C点坐标和B点坐标,根据三角形的面积公式得到bk=-18a,根据题意表示出D点坐标,得到b=6a,联立即可求出k的值.
解答 解: 作BE⊥x轴于E,DF⊥x轴于F,
作BE⊥x轴于E,DF⊥x轴于F,
设OA=a,AE=b,则C点坐标(-a,-$\frac{k}{a}$),B点坐标(-a-b,-$\frac{k}{a}$)
∵BD=2AD,
∴S△BCD=2S△ACD=6,
∴S△ACB=9=$\frac{1}{2}$AC•BC=$\frac{1}{2}$•(-$\frac{k}{a}$)•b,
整理得bk=-18a,
∵B点坐标(-a-b,-$\frac{k}{a}$),BD=2AD,
∴D点坐标(-$\frac{1}{3}$b-a,-$\frac{k}{3a}$),
∵点D在双曲线y=$\frac{k}{x}$上,
则(-$\frac{1}{3}$b-a)×(-$\frac{k}{3a}$)=k,
整理得,b=6a,
又∵bk=-18a,
∴k=-3.
故选:C.
点评 本题考查的是反比例函数系数k的几何意义,掌握反比例函数图象上点的坐标特征、灵活运用数形结合思想是解题的关键.

练习册系列答案
相关题目
5.下列运算结果正确的是( )
| A. | $\frac{a}{b}$÷$\frac{c}{d}$=$\frac{ac}{bd}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=1 | ||
| C. | ($\frac{2a}{a-b}$)2=$\frac{4{a}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{m}^{4}}{{n}^{5}}$•$\frac{{n}^{4}}{{m}^{3}}$=$\frac{m}{n}$ |
19.下列命题中真命题的有( )
①同位角相等;②在△ABC中,若∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
①同位角相等;②在△ABC中,若∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.下列运算正确的是( )
| A. | x3+x2=x5 | B. | x3-x2=x | C. | x3•x-2=x-5 | D. | x3÷x2=x |
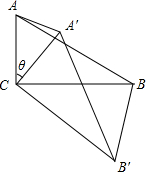 如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.