题目内容
6.阅读下面材料,再解方程:解方程x2-|x|-6=0
解:当x≥0时,原方程化为x2-x-6=0,解得:x1=3,x2=-2(不合题意,舍去);
当x<0时,原方程化为x2+x-6=0,解得:x1=-3(不合题意,舍去),x2=2;
∴原方程的根是x1=3,x2=2.
(1)请参照例题解方程x2-|x-1|-3=0;
(2)拓展应用:已知实数m,n满足:m2-7m+2=0,n2-7n+2=0,求:$\frac{n}{m}$+$\frac{m}{n}$的值.
分析 (1)分x≥1和x<1两种情形,把绝对值方程转化为一元二次方程解决.
(2)①当m=n时,$\frac{n}{m}$+$\frac{m}{n}$=2;
②当m≠n时,m、n是方程x2-7x+2=0的两根,根据根与系数关系即可解决问题.
解答 解:(1)当x≥1时,原方程化为x2-x-2=0,解得:x1=2,x2=-1(不合题意,舍去);
当x<1时,原方程化为x2+x-4=0,解得:x1=$\frac{-1-\sqrt{17}}{2}$,x2=$\frac{-1+\sqrt{17}}{2}$(不合题意,舍去),;
∴原方程的根是x1=2,x2=$\frac{-1-\sqrt{17}}{2}$.
(2)∵m2-7m+2=0,n2-7n+2=0,
①当m=n时,$\frac{n}{m}$+$\frac{m}{n}$=2,
②当m≠n时,m、n是方程x2-7x+2=0的两根,
∴m+n=7,mn=2,
∴原式=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{49-4}{2}$=$\frac{45}{2}$.
∴$\frac{n}{m}$+$\frac{m}{n}$的值为2或$\frac{45}{2}$.
点评 本题考查根与系数关系、整体代入的思想,解题的关键是学会转化的思想,把问题转化为一元二次方程解决,学会分类讨论的思想,学会利用公式恒等变形,属于中考常考题型.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.在平面直角坐标系中,将点(-2,3)关于原点的对称点向右平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
14.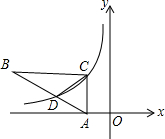 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
1.tan45°的值等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
11.在下列调查中,适宜采用普查的是( )
| A. | 了解某校九(1)班学生视力情况 | B. | 调查2016年央视春晚的收视率 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 了解我市中学生课余上网时间 |
18. 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
13.菱形ABCD中,对角线AC、BD相交于O,H为AD边中点,OH的长等于3,则菱形ABCD的周长为( )
| A. | 24 | B. | 12 | C. | 9 | D. | 18 |
 如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.
如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.