题目内容
9.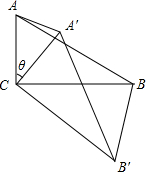 如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.
如图,在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°).得到△A′B′C.(1)连接A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′和S△BCB′,求证:S△ACA′:S△BCB′=1:3;
(2)M,N分别为A′A、B′B的中点,若AC=1,θ=120°,则MN的长度是1.
分析 (1)由旋转的性质可得△ACA′和△BCB′都是等腰三角形,并且∠ACA′=∠BCB′=30°,所以△ACA′∽△BCB′,根据相似三角形的面积比等于相似比的平方得到它们面积的比等于CA2:CB2;
(2)根据已知条件得到BC=$\sqrt{3}$,根据旋转的性质得到A′C=AC,B′C=BC,∠ACA′=∠BCB′=120°,求得∠CAM=∠CBN=30°,连接CM,CN,根据等腰三角形的性质得到CM⊥AA′,CN⊥BB′,根据直角三角形的性质得到CM=$\frac{1}{2}$AC=$\frac{1}{2}$,CN=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$,根据勾股定理即可得到结论.
解答 解:(1)∵△ABC绕顶点C顺时针旋转θ,得到△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=θ,
∴△ACA′∽△BCB′,
∴S△ACA′:S△BCB′=($\frac{AC}{BC}$)2=tan230°=$\frac{1}{3}$;
(2)∵∠ACB=90°,∠ABC=30°,AC=1,
∴BC=$\sqrt{3}$,
∵将△ABC绕顶点C顺时针旋转,旋转角为120°,
∴A′C=AC,B′C=BC,∠ACA′=∠BCB′=120°,
∴∠CAM=∠CBN=30°, 如图2,连接CM,CN,
如图2,连接CM,CN,
∵M,N分别为A′A、B′B的中点,
∴CM⊥AA′,CN⊥BB′,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$,CN=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$,
∵∠NCM=120°+90°-60°-60°=90°,
∴MN=$\sqrt{C{N}^{2}+C{M}^{2}}$=1.
故答案为:1.
点评 本题考查了相似三角形的判定与性质:有两组对应边的比相等,并且它们的夹角相等的两三角形相似;相似三角形的面积的比等于相似比的平方.也考查了旋转的性质.

 阅读快车系列答案
阅读快车系列答案| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
| A. | -3 | B. | 2 | C. | -1 | D. | 0 |
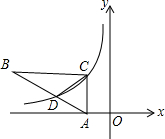 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
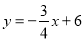 与
与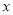 轴、
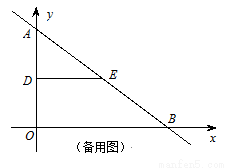
轴、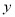 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为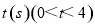 .
.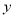 (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;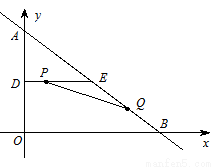
 如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题:
如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题: