题目内容
17. 如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧.
如图,以?ABCD的一边为直径⊙O,恰好与边CD相切于点D,E是⊙O上一点,点E与点D位于直径AB的两侧.①求∠AED的度数;
②若⊙O的半径为5cm,AE=8cm,求tan∠ADE的值.
分析 ①先证明∠AOD=90°,再根据∠AED=$\frac{1}{2}$∠AOD即可解决问题.
②根据tan∠ADE=tan∠ABE,求出BE即可解决问题.
解答 解:①如图, 连接OD、BE.
连接OD、BE.
∵CD是⊙O切线,
∴CD⊥OD,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴OD⊥AB,
∴∠AOD=90°,
∴∠AED=$\frac{1}{2}$∠AOD=45°.
②∵AB是直径,
∴∠AEB=90°,
∵AB=10,AE=8,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵∠ADE=∠ABE,
∴tan∠ADE=tan∠ABE=$\frac{AE}{BE}$=$\frac{4}{3}$.
点评 本题考查切线的性质、平行四边形的性质、勾股定理、同弧所对的圆周角与圆心角的关系等知识,解题的关键是熟练掌握这些知识的应用,属于中考常考题型.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
8.下列图中∠1和∠2是同位角的是( )


| A. | ①、②、③ | B. | ②、③、④ | C. | ③、④、⑤ | D. | ①、②、⑤ |
12. 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
2.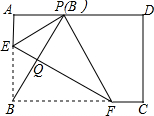 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )
如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④若P是AD的中点,则矩形ABCD为正方形.其中正确的是( )| A. | ①④ | B. | ①③ | C. | ②③ | D. | ①③④ |
9. 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )| A. | AB=CD | B. | AO=CO | C. | AC=BD | D. | BO=DO |
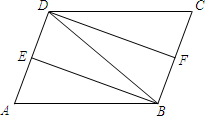 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.
如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.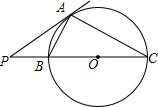 如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.
如图,PA是⊙O的切线,割线PBC与⊙O相交于点B、C,PA=6、PB=4,则BC=5.$\frac{AB}{AC}$的值为$\frac{2}{3}$.