题目内容
20.画出符合下列条件的一次函数y=kx+b的大致图象.(1)k>0,b>0;
(2)k>0,b<0;
(3)k<0,b>0;
(4)k<0,b<0.
分析 (1)由k>0、b>0结合一次函数图象与系数的关系即可得出一次函数y=kx+b的图象过第一、二、三象限,画出大致图象即可;
(2)由k>0、b<0结合一次函数图象与系数的关系即可得出一次函数y=kx+b的图象过第一、三、四象限,画出大致图象即可;
(3)由k<0、b>0结合一次函数图象与系数的关系即可得出一次函数y=kx+b的图象过第一、二、四象限,画出大致图象即可;
(4)由k<0、b<0结合一次函数图象与系数的关系即可得出一次函数y=kx+b的图象过第二、三、四象限,画出大致图象即可.
解答 解:(1)当k>0,b>0时,一次函数y=kx+b的图象过第一、二、三象限,
如图(1)所示;
(2)当k>0,b<0时,一次函数y=kx+b的图象过第一、三、四象限,
如图(2)所示;
(3)当k<0,b>0时,一次函数y=kx+b的图象过第一、二、四象限,
如图(3)所示;
(4)当k<0,b<0时,一次函数y=kx+b的图象过第二、三、四象限,
如图(4)所示.
点评 本题考查了一次函数图象与系数的关系,解题的关键是:(1)k>0,b>0?y=kx+b的图象在一、二、三象限;(2)k>0,b<0?y=kx+b的图象在一、三、四象限;(3)k<0,b>0?y=kx+b的图象在一、二、四象限;(4)k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
15.先阅读下面的材料,再解答后面的问题.
现代社会对保密要求越来越高,密码正在成为人们生活的一部分,有一种密码的明文(真实文)按计算器键盘字母排列分解,其中Q、W、E、…、N、M这26个字母依次对应1、2、3…、25、26这26个自然数(见表):
给出一个变换公式:$\left\{\begin{array}{l}x'=\frac{x}{3}(x是自然数,1≤x≤26,x被3整除)\\ x'=\frac{x+2}{3}+17(x是自然数,1≤x≤26,x被3除余1)\\ x'=\frac{x+1}{3}+8(x是自然数,1≤x≤26,x被3除余2)\end{array}\right.$
如:将明文R转换成密文,R→4(4被3除余1)→$\frac{4+2}{3}$+17=19→L,即R变为L.
将明文A转换成密文,A→11(11被3除余2)→$\frac{11+1}{3}$+8=12→S,即A变为S.
再如:将密文X转换成明文,X→21→3×(21-17)-2=10→P,即X变为P;
将密文D转换成明文,D→13→3×(13-8)-1=14→F,即D变为F;
(1)按上述方法将明文NET译为密文;
(2)若按上述方法将明文译成的密文为DMN,请找出它的明文.
现代社会对保密要求越来越高,密码正在成为人们生活的一部分,有一种密码的明文(真实文)按计算器键盘字母排列分解,其中Q、W、E、…、N、M这26个字母依次对应1、2、3…、25、26这26个自然数(见表):
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
如:将明文R转换成密文,R→4(4被3除余1)→$\frac{4+2}{3}$+17=19→L,即R变为L.
将明文A转换成密文,A→11(11被3除余2)→$\frac{11+1}{3}$+8=12→S,即A变为S.
再如:将密文X转换成明文,X→21→3×(21-17)-2=10→P,即X变为P;
将密文D转换成明文,D→13→3×(13-8)-1=14→F,即D变为F;
(1)按上述方法将明文NET译为密文;
(2)若按上述方法将明文译成的密文为DMN,请找出它的明文.
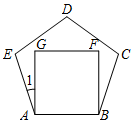 有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.
有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.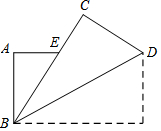 如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法: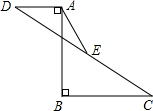 如图,AB⊥BC于点B,AB⊥AD于点A,AD=5,AB=12,BC=10,E是CD的中点,则AE的长是6.5.
如图,AB⊥BC于点B,AB⊥AD于点A,AD=5,AB=12,BC=10,E是CD的中点,则AE的长是6.5.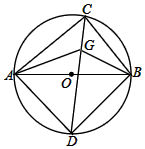 如图,AB为⊙O的直径,C为上半圆上一点,D为下半圆弧的中点,G为CD上一点,满足DA=DG
如图,AB为⊙O的直径,C为上半圆上一点,D为下半圆弧的中点,G为CD上一点,满足DA=DG