题目内容
5.已知方程组$\left\{\begin{array}{l}{{a}_{1}x+y={c}_{1}}\\{{a}_{2}x+y={c}_{2}}\end{array}\right.$解为$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$,则关于x,y的方程组$\left\{\begin{array}{l}{3{a}_{1}x+2y={a}_{1}+{c}_{1}}\\{3{a}_{2}x+2y={a}_{2}+{c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$.分析 根据方程组解的定义,把x=5,y=10代入即可得出a1,a2,c1,c2的关系,再代入计算即可.
解答 解:∵方程组$\left\{\begin{array}{l}{{a}_{1}x+y={c}_{1}}\\{{a}_{2}x+y={c}_{2}}\end{array}\right.$解为$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$,
∴$\left\{\begin{array}{l}{5{a}_{1}+10={c}_{1}}\\{5{a}_{2}+10={c}_{2}}\end{array}\right.$,
∵$\left\{\begin{array}{l}{3{a}_{1}x+2y={a}_{1}+{c}_{1}}\\{3{a}_{2}x+2y={a}_{2}+{c}_{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{3{a}_{1}x+2y=6{a}_{1}+10①}\\{3{a}_{2}x+2y=6{a}_{2}+10②}\end{array}\right.$,
①-②,得3a1x-3a2x=6a1-6a2,
∴x=2,
把x=2代入①得,y=5,
∴方程组$\left\{\begin{array}{l}{3{a}_{1}x+2y={a}_{1}+{c}_{1}}\\{3{a}_{2}x+2y={a}_{2}+{c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,
故答案为$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$.
点评 本题考查了解二元一次方程组,掌握方程组的解法是解题的关键.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
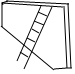 (1)如图,长3m的梯子斜靠着墙,梯子底端离墙底0.6m,问梯子顶端离地面多少米?(精确到0.1m)
(1)如图,长3m的梯子斜靠着墙,梯子底端离墙底0.6m,问梯子顶端离地面多少米?(精确到0.1m)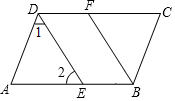 如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.
如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.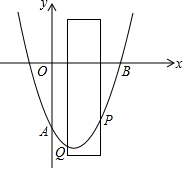 如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.
如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.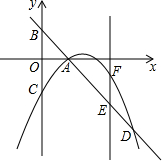 如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.
如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.