题目内容
19.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,位似比为2:1将△EFO缩小,则点E的对应点E′的坐标是(-2,1)或(2,-1).分析 若位似比是k,则原图形上的点(x,y),经过位似变化得到的对应点的坐标是(kx,ky)或(-kx,-ky).
解答 解:∵点E(-4,2),F(-2,-2),以原点O为位似中心,位似比为2:1将△EFO缩小,
∴点E的对应点E′的坐标是:(-2,1)或(2,-1).
故答案为:(-2,1)或(2,-1).
点评 此题考查了位似图形的性质,注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标比等于±k.

练习册系列答案
相关题目
14.若△ABC∽△DEF,他们的面积比为1:4,则△ABC与△DEF的相似比为( )
| A. | 1:4 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
8.已知m和n是方程2x2-5x-3=0的两根,则$\frac{1}{m}$+$\frac{1}{n}$的值是( )
| A. | -2 | B. | 2 | C. | -$\frac{5}{3}$ | D. | 1 |
9.在下列二次根式中,与$\sqrt{27}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{18}$ |
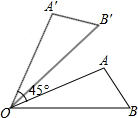 如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.
如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角.那么,线段AB的对应线段是线段A′B′;线段OB的对应线段是线段OB′;∠A的对应角是∠A′.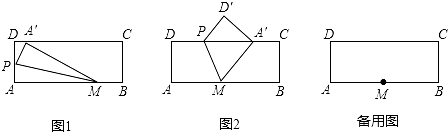
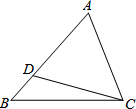 如图,在△ABC中,D是AB上一点,∠ACD=∠B,AC=$\sqrt{6}$,DB=1,则AD的长是2.
如图,在△ABC中,D是AB上一点,∠ACD=∠B,AC=$\sqrt{6}$,DB=1,则AD的长是2.