题目内容
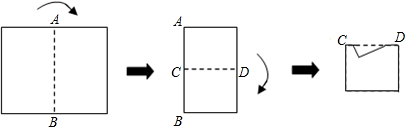
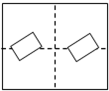
12. 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.(1)作线段BD的垂直平分线,分别交AD、BC于点E、F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接BE、DF,问四边形BEDF是什么特殊四边形?请说明理由.
分析 (1)作线段BD的垂直平分线即可解决问题;
(2)只要证明四边相等即可解决问题;
解答 解:(1)如图,直线EF即为所求.
(2)四边形BEDF是菱形.
理由如下:∵EF垂直平分BD,
∴BE=DE,BF=DF,
∴∠DEB=∠BEF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
∴BE=BF,
∴BE=BF=DF=DE,
∴四边形BEDF是菱形.
点评 本题考查基本作图、矩形的性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.计算(x+2)(x-2)结果正确的是( )
| A. | x2-4 | B. | x2-2 | C. | 4-x2 | D. | x2+2 |
1. 如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
 如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
 已知:如图,AD=BC,AC=BD,求证:△ABC≌△BAD.
已知:如图,AD=BC,AC=BD,求证:△ABC≌△BAD.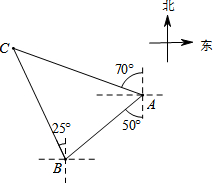 如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度. 在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.
在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.