题目内容
7.(1)计算:$\sqrt{8}$+(2016-$\sqrt{5}$)0-2-1-4cos45°.(2)化简求值:$\frac{{x}^{2}}{x-1}-\frac{1}{x-1}$,其中x=2015.
分析 (1)分别根据0指数幂、负整数指数幂的计算法则、特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分母不变,把分子相加减,再把x的值代入进行计算即可.
解答 解:(1)原式=2$\sqrt{2}$+1-$\frac{1}{2}$-4×$\frac{\sqrt{2}}{2}$
=2$\sqrt{2}$+$\frac{1}{2}$-2$\sqrt{2}$
=$\frac{1}{2}$;
(2)原式=$\frac{{x}^{2}-1}{x-1}$=$\frac{(x+1)(x-1)}{x-1}$=x+1,
当x=2015时,原式=2016.
点评 本题考查的是分式的化简求值及实数的运算,熟知0指数幂、负整数指数幂的计算法则、特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
17. 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )| A. | BE⊥CE | B. | BF∥CE | C. | BE=CF | D. | AB=AC |
18.下列四个实数最小的是( )
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
12.一枚质地均匀的六面骰子,六个面上分别刻有1,2,3,4,5,6点,投掷一次得到的点数为奇数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19. 如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
 如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
 如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )
如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )



 在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).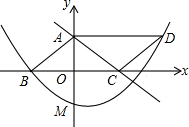 如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.
如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.