��Ŀ����
17��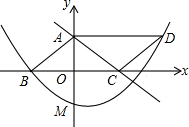 ��ͼ��ƽ���ı���ABCD�У�D����������y=$\frac{1}{8}$x2+bx+c�ϣ���OB=OC��AB=5��tan��ACB=$\frac{3}{4}$��M����������y��Ľ��㣮
��ͼ��ƽ���ı���ABCD�У�D����������y=$\frac{1}{8}$x2+bx+c�ϣ���OB=OC��AB=5��tan��ACB=$\frac{3}{4}$��M����������y��Ľ��㣮��1����ֱ��AC�������ߵĽ���ʽ��
��2������P��A��D��ͬʱ����Q��C��A����ÿ��1����λ���ٶ��˶����ʣ���P�˶����δ�ʱ����APQ��ֱ�������Σ�
��3���ڣ�2���е�P�˶���ij��ʱ���ı���PDCQ�������С�����ʱ��CMQ�������
���� ��1����������������Ǻ�����ϵ�ó�A��C�����꣬�����һ�κ�������ʽ������ƽ���ı��ε������������D���꣬���ô���ϵ���������b��c��ֵ���̶��ó����κ�������ʽ��
��2�����P�˶���t��ʱ��PQ��AC����ʱAP=t��CQ=t��AQ=5-t�����ɡ�APQ�ס�CAO���AQP�ס�CAO�����ö�Ӧ�߳ɱ��������t��ֵ���̶�ȷ����P��λ�ã�
��3��ֻ��ʹ��APQ���������������ı���PDCQ�������С�����APQ�ױ�AP�ϵĸ�Ϊh����QH��AD�ڵ�H���ɡ�AQH�ס�CAO�����ö�Ӧ�߳ɱ����ó�h�ı���ʽ���̶���ʾ����APQ���������ʽ�����ɵó��ı���PDCQ����Сֵ��Ҳ��ȷ����P��λ�ã������ó�Q��λ�ã������ó���CMQ�������
���  �⣺��1����ͼ1����tan��ACB=$\frac{3}{4}$��
�⣺��1����ͼ1����tan��ACB=$\frac{3}{4}$��
��$\frac{AO}{CO}$=$\frac{3}{4}$��
����AO=3x��CO=4x����OB=OC��
��BO=4x��
��AB2=AO2+BO2��
��25=25x2��
��ã�x=1��������ȥ����
��AO=3��BO=CO=4��
��A��0��3����B��-4��0����C��4��0����
����ֱ��AC�Ľ���ʽΪ��y=kx+d��
��$\left\{\begin{array}{l}{d=3}\\{4k+d=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{d=3}\\{k=-\frac{3}{4}}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪ��y=-$\frac{3}{4}$x+3��
���ı���ABCD��ƽ���ı��Σ�
��BC=AD=8��
��D��8��3����
��B��D�㶼��������y=$\frac{1}{8}$x2+bx+c�ϣ�
��$\left\{\begin{array}{l}{\frac{1}{8}��64+8b+c=3}\\{\frac{1}{8}��16-4b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-\frac{1}{4}}\\{c=-3}\end{array}\right.$��
�ʴ������߽���ʽΪ��y=$\frac{1}{8}$x2-$\frac{1}{4}$x-3��
��2������ͼ2����OA=3��OB=4��
��AC=5��
���P�˶���t��ʱ��PQ��AC����ʱAP=t��CQ=t��AQ=5-t��
��PQ��AC��
���AQP=��AOC=90�㣬��PAQ=��ACO��
���APQ�ס�CAO��
��$\frac{AP}{AC}$=$\frac{AQ}{CO}$����$\frac{t}{5}$=$\frac{5-t}{4}$��
��ã�t=$\frac{25}{9}$��
����ͼ3�����P�˶���t��ʱ����QP��AD����ʱAP=t��CQ=t��AQ=5-t��
��QP��AD��
���APQ=��AOC=90�㣬��PAQ=��ACO��
���AQP�ס�CAO��
��$\frac{AQ}{AC}$=$\frac{AP}{CO}$����$\frac{5-t}{5}$=$\frac{t}{4}$��
��ã�t=$\frac{20}{9}$��
������P�˶�������A��$\frac{25}{9}$��$\frac{20}{9}$����λ���ȴ�����APQ��ֱ�������Σ�
��3����ͼ4����S�ı���PDCQ+S��APQ=S��ACD����S��ACD=$\frac{1}{2}$��8��3=12��
�൱��APQ��������ʱ���ı���PDCQ�������С��
������P�˶�t��ʱ��AP=t��CQ=t��AQ=5-t��
���APQ�ױ�AP�ϵĸ�Ϊh����QH��AD�ڵ�H��
�ɡ�AQH�ס�CAO�ɵã�$\frac{h}{3}$=$\frac{5-t}{5}$��
��ã�h=$\frac{3}{5}$��5-t����
��S��APQ=$\frac{1}{2}$t��$\frac{3}{5}$��5-t��=$\frac{3}{10}$��-t2+5t��=-$\frac{3}{10}$��t-$\frac{5}{2}$��2+$\frac{15}{8}$��
�൱t=$\frac{5}{2}$ʱ��S��APQ�ﵽ���ֵ$\frac{15}{8}$����ʱS�ı���PDCQ=12-$\frac{15}{8}$=$\frac{81}{8}$��
�ʵ���P�˶��������A��$\frac{5}{2}$����λ��ʱ���ı���PDCQ�����С��
��AQ=QC=$\frac{5}{2}$��
�ʡ�CMQ�����Ϊ��$\frac{1}{2}$S��AMC=$\frac{1}{2}$��$\frac{1}{2}$��4��6=6��
���� ���⿼���˶��κ������ۺϣ��漰�˴���ϵ������������ʽ��ƽ���ı��ε����ʡ����������ε��ж������ʣ������Ĺؼ����ҵ���������ʱ�����������Σ����ö�Ӧ�߳ɱ�����֪ʶ�ó��й��߶εij��Ȼ����ʽ���ѶȽϴ�

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�| A�� | y��0 | B�� | y��0 | C�� | y��1 | D�� | 0��y��1 |
| A�� | 159��163 | B�� | 157��161 | C�� | 159��159 | D�� | 159��161 |
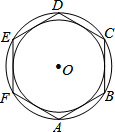 ��ͼ����������ABCDEF�ı߳�Ϊ2������������ε����Բ������Բ���γɵ�Բ�����Ϊ�У�
��ͼ����������ABCDEF�ı߳�Ϊ2������������ε����Բ������Բ���γɵ�Բ�����Ϊ�У� ��ͼ��ʾ��ͼ����������y=ax2+2ax+a2+2��һ���֣�����x���һ������A�������ǣ�-3��0����������x�����һ�����������Ϊ��1��0����
��ͼ��ʾ��ͼ����������y=ax2+2ax+a2+2��һ���֣�����x���һ������A�������ǣ�-3��0����������x�����һ�����������Ϊ��1��0����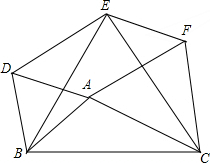 ��ͼ��ʾ���ԡ�ABC������AB��BC��CA��BC��ͬ�����ȱߡ�ABD����BCE����CAF
��ͼ��ʾ���ԡ�ABC������AB��BC��CA��BC��ͬ�����ȱߡ�ABD����BCE����CAF