题目内容
12.已知二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,其顶点为A,与x轴两交点为B、C.(1)求B、C两点的坐标.
(2)求△ABC的面积.
分析 (1)根据函数图象关于y轴对称,可得m的值,根据函数值为零,可得关于x的方程,根据解方程,可得B、C点坐标;
(2)根据自变量为零时,可得A点坐标,根据三角形面积公式,可得答案.
解答 解:由二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,得
m-1=0.
解得m=1.
函数解析式为y=-x2+1,
当y=0时,-x2+1=0.
解得x1=-1,x2=1,
即B(-1,0),C(1,0);
(2)当x=0时,y=1,即A(0,1),
S△ABC=$\frac{1}{2}$×2×1=1.
点评 本题考查了二次函数的性质,利用对称轴得出m的值是解题关键,又利用了自变量与函数值的对应关系得出A、B、C的坐标,最后利用了三角形的面积公式.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
5.等腰三角形的底角为50°,则这个等腰三角形的顶角为( )
| A. | 50° | B. | 80° | C. | 100° | D. | 50°或80° |
4.已知坐标原点为O,点A(2,1),将OA绕原点O顺时针旋转90°后,A的对应点A1的坐标是( )
| A. | (2,-1) | B. | (-2,1) | C. | (1,-2) | D. | (-1,2) |
2.在下列运算中,正确的是( )
| A. | 4x+2y=6xy | B. | 2x3•x2=2x5 | C. | (x2)3=x5 | D. | (3xy)2÷(xy)=3xy |
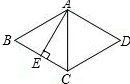 如图,菱形ABCD的边长为2,高AE平分BC,求:
如图,菱形ABCD的边长为2,高AE平分BC,求: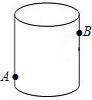 如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.
如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.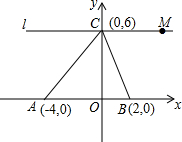 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)