题目内容
7.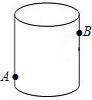 如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.
如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.
分析 先把圆柱沿过B点的母线剪开,然后展开如图,A′点为点A展开后的对应点,根据两点之间线段最短得到最短路线长度为A′B的长度,然后根据勾股定理计算A′B的长即可.
解答  解:把圆柱沿过B点的母线剪开,然后展开如图,A′点为点A展开后的对应点,
解:把圆柱沿过B点的母线剪开,然后展开如图,A′点为点A展开后的对应点,
作BH⊥MN于H,BH=$\frac{1}{2}$×48=24,MH=1,A′N=1,
∴A′H=20-1-1=18,
在Rt△A′BH中,A′B=$\sqrt{A′{H}^{2}-B{H}^{2}}$=30(cm).
故答案为30cm.
点评 本题考查了平面展开-最短路径问题:先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
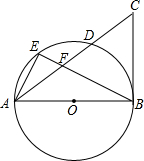 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D. E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB
如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D. E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB 如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.
如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.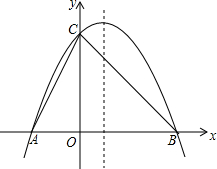 如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC.
如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC.