题目内容
4.已知坐标原点为O,点A(2,1),将OA绕原点O顺时针旋转90°后,A的对应点A1的坐标是( )| A. | (2,-1) | B. | (-2,1) | C. | (1,-2) | D. | (-1,2) |
分析 过A作AC⊥y轴于C,过A1作A1D⊥y轴于D,根据旋转求出∠A=∠A1OD,证△AC0≌△ODA1,推出A1D=OC=1,OD=CA=2即可.
解答  解:过A作AC⊥y轴于C,过A1作A1D⊥y轴于D.
解:过A作AC⊥y轴于C,过A1作A1D⊥y轴于D.
∵∠AOA1=90°,∠ACO=90°,
∴∠AOC+∠A1OD=90°,∠A+∠AOC=90°,
∴∠A=∠A1OD,
在△AC0和△ODA1中
∵$\left\{\begin{array}{l}{∠OCA=∠OD{A}_{1}}\\{∠CAO=∠{A}_{1}OD}\\{OA=O{A}_{1}}\end{array}\right.$,
∴△AC0≌△ODA1(AAS),
∴A1D=OC=1,OD=CA=2,
∴A1的坐标是(1,-2).
故选:C.
点评 本题主要考查对坐标与图形变换-旋转,全等三角形的性质和判定等知识点的理解和掌握,能正确画出图形并求出△AC0≌△ODA1是解此题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
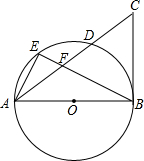 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D. E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB
如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D. E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB
 如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.
如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.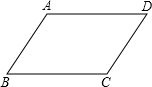 如图,在?ABCD中,AB=8,AD=10,过点A的直线交边BC所在的直线为点E,交DC所在的直线为点F,若CE=2,则DF的长为10或$\frac{20}{3}$.
如图,在?ABCD中,AB=8,AD=10,过点A的直线交边BC所在的直线为点E,交DC所在的直线为点F,若CE=2,则DF的长为10或$\frac{20}{3}$.