题目内容
19.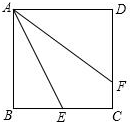 如图,正方形ABCD中,E为BC上的一点,DF=CF,DC+CE=AE,求证:AF平分∠DAE.
如图,正方形ABCD中,E为BC上的一点,DF=CF,DC+CE=AE,求证:AF平分∠DAE.
分析 延长AF交BC的延长线于点G,由正方形的性质及DF=CF就可以得出△ADF≌△GCF,就有AD=CG,∠DAF=∠G,进而得出CG=DC,得出AE=EG,就有∠EAF=∠G,得出∠EAF=∠DAF,从而得出结论.
解答 证明:延长AF交BC的延长线于点G.
∵四边形ABCD是正方形,
∴AD=BC=CD,∠D=∠BCD=90°.AD∥BC,
∴∠D=∠GCF.∠AFD=∠GFC.
在△ADF和△GCF中,
$\left\{\begin{array}{l}{∠D=∠GCF}\\{DF=CF}\\{∠AFD=∠GFC}\end{array}\right.$,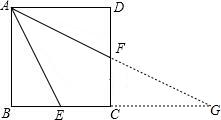
∴△ADF≌△GCF(ASA),
∴AD=GC,∠DAF=∠G,
∴CD=GC.
∵DC+CE=AE,
∴CG+CE=AE,
∴EG=AE,
∴∠EAF=∠G
∴∠EAF=∠DAF,
∴AF平分∠DAE.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,角平分线的判定的运用,等腰三角形的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,AB=AC,点F、E分别是AB、AC的中点.求证:∠1=∠2.
如图,AB=AC,点F、E分别是AB、AC的中点.求证:∠1=∠2.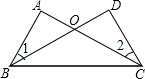 如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.
如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.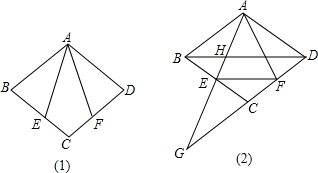
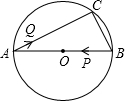 如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为3-$\sqrt{3}$,$\frac{32-8\sqrt{3}}{13}$.
如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为3-$\sqrt{3}$,$\frac{32-8\sqrt{3}}{13}$.