Question

18．（1）如图①在△ABC，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到AB的距离是2cm
（2）如图②，已知∠1=∠2，∠3=∠4，求证：AP平分∠BAC．

Answer 1

分析 （1）根据题意求出DC，根据角平分线的性质解答；
（2）作PD⊥AB于D，PE⊥BC于E，PF⊥AC于F，根据角平分线的性质定理和判定定理证明即可．

解答 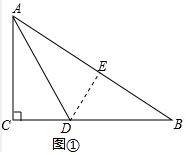解：（1）如图①，作DE⊥AB于E，
∵BC=6cm，BD=4cm，
∴CD=2cm，
∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴DE=CD=2cm，即点D到AB的距离是2cm，
故答案为：2；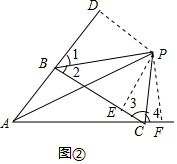
（2）证明：如图②，作PD⊥AB于D，PE⊥BC于E，PF⊥AC于F，
∵∠1=∠2，PD⊥AB，PE⊥BC，
∴PD=PE，
同理，PF=PE，
∴PD=PF，又PD⊥AB，PF⊥AC，
∴AP平分∠BAC．

点评 本题考查的是角平分线的性质和判定，掌握角的平分线上的点到角的两边的距离相等是解题的关键．